Given three straight lines $2 x + 11 y - 5 = 0, 24 x + 7 y - 20 = 0,$ and $4 x - 3 y - 2 = 0$ . Then, they form a triangle one line bisects the angle between the other two two of them are parallel

A

12 and 4 respectively

B

11 and 5 respectively

C

Equal to each other

D

Not equal to each other

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

We know, the perpendicular distance (d) from point $(x_{1}, y_{2})$ to line $a x + b y + c = 0$ is $\frac{| a x_{1} + b y_{1} + c |}{\sqrt{a^{2} + b^{2}}}$ .
Let us find a point on line $2 x + 11 y - 5 = 0$ .
for $x = 0, 2 (0) + 11 y - 5 = 0$
$\Rightarrow 11 y - 5 = 0$
$\Rightarrow y = \frac{5}{11}$ .
So, $(x, y) = (0, \frac{5}{11})$
Let us find perpendicular distances of this point to the gives lines.

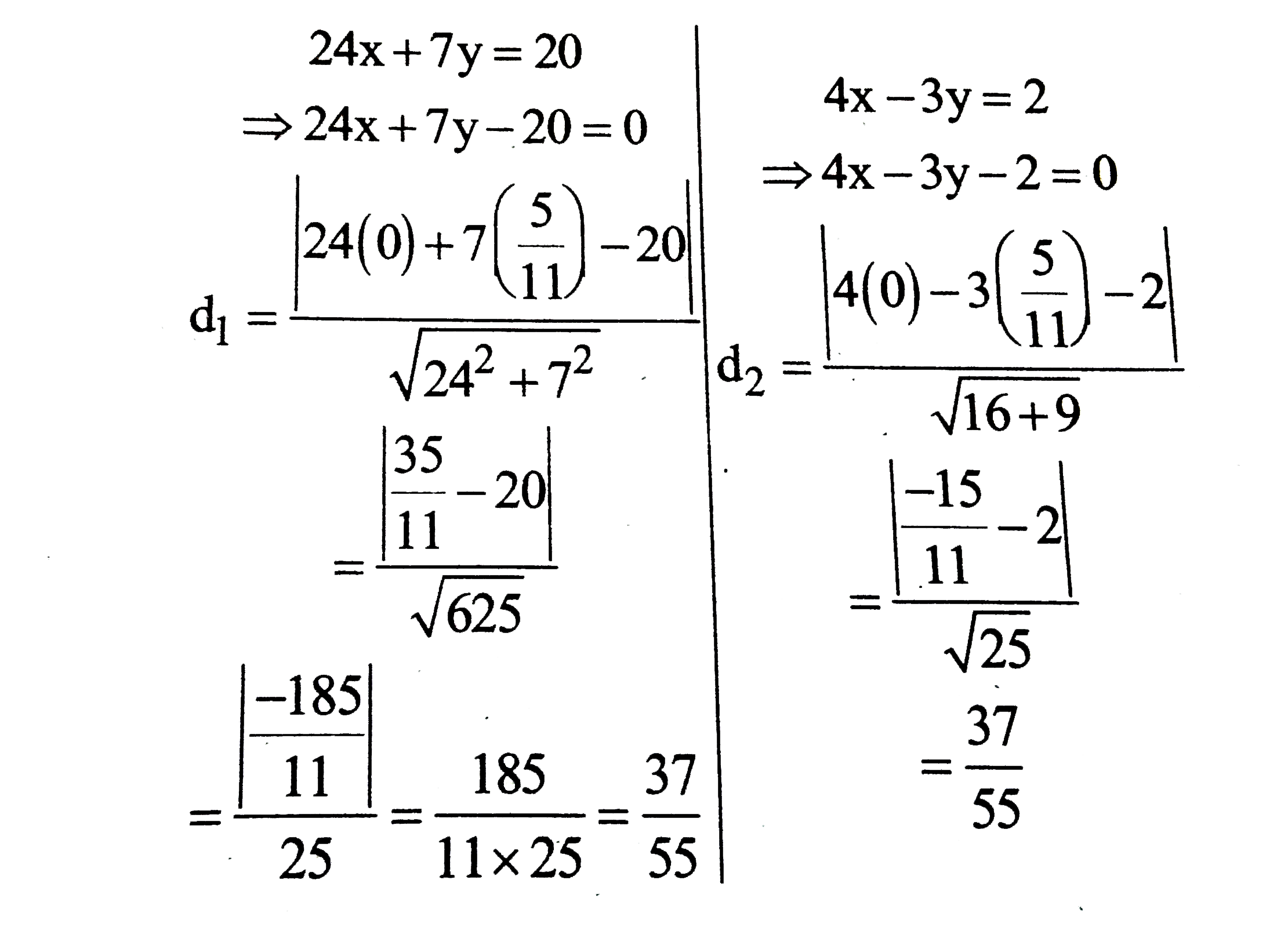
$∴ d_{1} = d_{2}$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
The three straight lines $2 x + 11 y - 5 = 0, 24 x + 7 y = 20$ and $4 x - 3 y - 2 = 0$ are such that
Athey form a triangle
Bthey are all concurrent
Cone of them is a bisector of the other two
Dnone
Question 2 - Select One
Three straight lines
2x + 11y - 5 = 0
24x + 7y - 20 = 0
4x - 3y - 2 = 0
Aform a triangle
Bare only concurrent
Care concurrent with one line bisecting the angle between the other two
DNone of the above
Question 3 - Select One
The straight lines $4 x - 3 y - 5 = 0, x - 2 y = 0, 7 x + y - 40 = 0$ and $x + 3 y + 10 = 0$ from
Aa rectangle
Ba parallelogram
Ca cyclic quadrilateral
Dnone of these

NDA PREVIOUS YEARS-CARTESIAN COORDINATE SYSTEM AND STRAIGHT LINE-MATHS

Home
Ask Doubt
Profile