The equation of the line, when the portion of it intercepted between the axes is divided by the point (2, 3) in the ratio of 3 : 2, is

A

Either $x + y or 9 x + y = 12$

B

Either $x + y = 5 or 4 x + 9 y = 30$

C

Either $x + y = 4 or x + 9 y = 12$

D

Either $x + y = 5 or 9 x + 4 y = 30$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Intercept form of line is $\frac{x}{a} + \frac{y}{b} = 1$ .
We know, the point which divides a line joining two points $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ in the ratio $m : n$ is

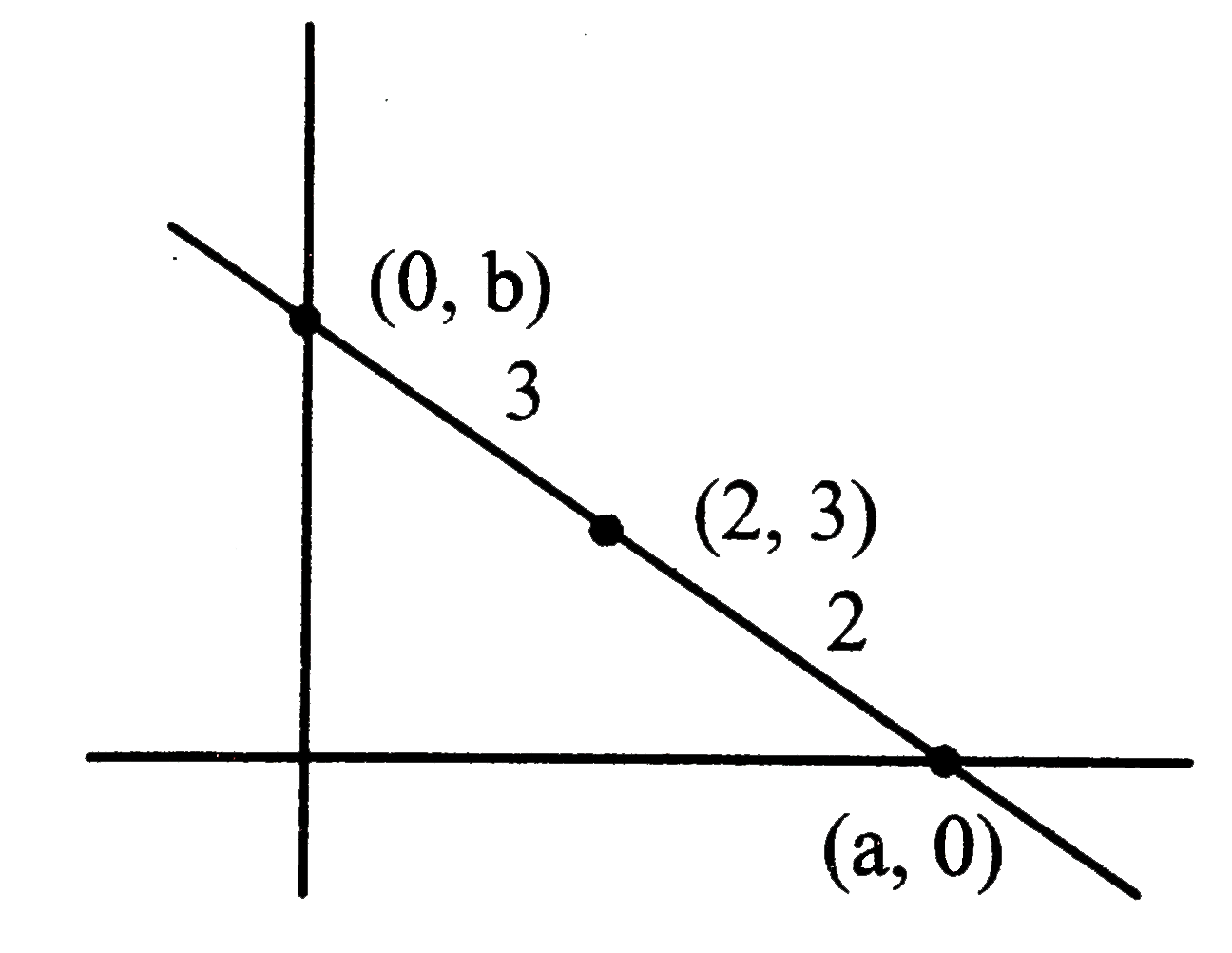
$(\frac{m x_{2} + n x_{1}}{m + n}, \frac{m y_{2} + n y_{1}}{m + n})$
Case 1 : $m : n = 2 : 3$
$∴ (2, 3) = (\frac{(2) (a) + 3 (0)}{2 + 3}, \frac{2 (0) + 3 (b)}{2 + 3})$
$\Rightarrow (2, 3) = (\frac{2 a}{5}, \frac{3 b}{5})$
$\Rightarrow \frac{2 a}{5} = 2, \frac{3 b}{5} = 3$
$\Rightarrow a = 5, b = 5$ .
$∴$ Equation of line is $\frac{x}{5} + \frac{y}{5} = 1 \Rightarrow x + y = 5$
Case 2 : $m : n = 3 : 2$
$∴ (2, 3) = (\frac{3 (a) + 2 (0)}{3 + 2}, \frac{3 (0) + 2 (b)}{3 + 2})$
$\Rightarrow (2, 3) = (\frac{3 a}{5}, \frac{2 b}{5})$
$\Rightarrow \frac{3 a}{5} = 2, \frac{2 b}{5} = 3$
$\Rightarrow a = \frac{10}{3}, b = \frac{15}{2}$
$∴$ Equation of line is $\frac{x}{\frac{10}{3}} + \frac{y}{\frac{15}{2}} = 1$
$\Rightarrow \frac{3 x}{10} + \frac{2 y}{15} = 1$
$\Rightarrow 9 x + 4 y = 30$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The equation straight line such that the portion of it intercepted between the coordinate axes is bisected at the point (h,k) is :
A $\frac{x}{h} + \frac{y}{k} = - 1$
B $\frac{x}{h} + \frac{y}{k} = 2$
C $\frac{x}{h} + \frac{y}{k} = 1$
D $\frac{x}{h} + \frac{y}{k} = - 1$

NDA PREVIOUS YEARS-CARTESIAN COORDINATE SYSTEM AND STRAIGHT LINE-MATHS

Home
Ask Doubt
Profile