The compressibility of gas < unity at STP.Therefore
Vm=22.4L
Vm<22.4L
Vm>22.4L
Vm=44.8L
Step by step video & image solution for The compressibility of gas < unity at STP.Therefore V_(m)=22.4 LV_(m)<22.4LV_(m)>22.4LV_(m)=44.8L by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
One of the important approach of the study of real gases involves the analysis of a parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume ,T is absolute temperature and R is the universal gas constant .Such a relation can also be expressed as Z=(V m realVm ideal) (where Vm ideal and V_("m real")arethemo≤rvolumeforalandrealgasrespectivelytendenciesamongconstituentpartic≤s.Aspressureisforceamongisloweredortemperatureis∈creasedthevalueofZapproachesalbehaviour<br>Forarealgas'G',Zgt1 at STP, then for 'G' which of the following is true ?
A1mole of the gas occupies 22.7 L at STPB1 mole of the gas occupies 22.7 L at pressure higher then that at STP (Keeping temperature constant )C1 Mole of the gas occupies 22.7 L at pressure lower then that at STP (keeping temperature constant )DNone of the above - Question 2 - Select One
One of the important approach of the study of real gases involves the analysis of a parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume ,T is absolute temperature and R is the universal gas constant .Such a relation can also be expressed as Z=(V m realVm ideal) (where Vm ideal and V_("m real") are the moler volume for ideal and real gas respectively tendencies among constituent particles.As pressure is force among is lowered or temperature is increased the value of Z approaches ideal behaviour
Choose the conslusions which are appropriate for the observation stated
AAll conclusions are trueBConclusions I, II and IV are tureCConclusions I,III and IV are trueDCinclusions III and Iv are true - Question 3 - Select One
Consider the following statements PVm=RT(1+BVm+BV2m+...) Then Vm .
Ais independent of temperatureBis equal to RTP to Boyle temperatureChas the dimension of molar volumeDNone of these
The van der Waals' equation for one mole may be expressed as
V3M−(b+RTP)V2m+aVmP−abP=0
where Vm is the molar volume of the gas. Which of the followning is incorrect?View SolutionAn AC source is connected in parallel with an L-C-R circuit as shown.Let ls,lL,lC and lR denote the currents through and Vs,VL,VC and VRthe voltage across the corresponding componts.Then,
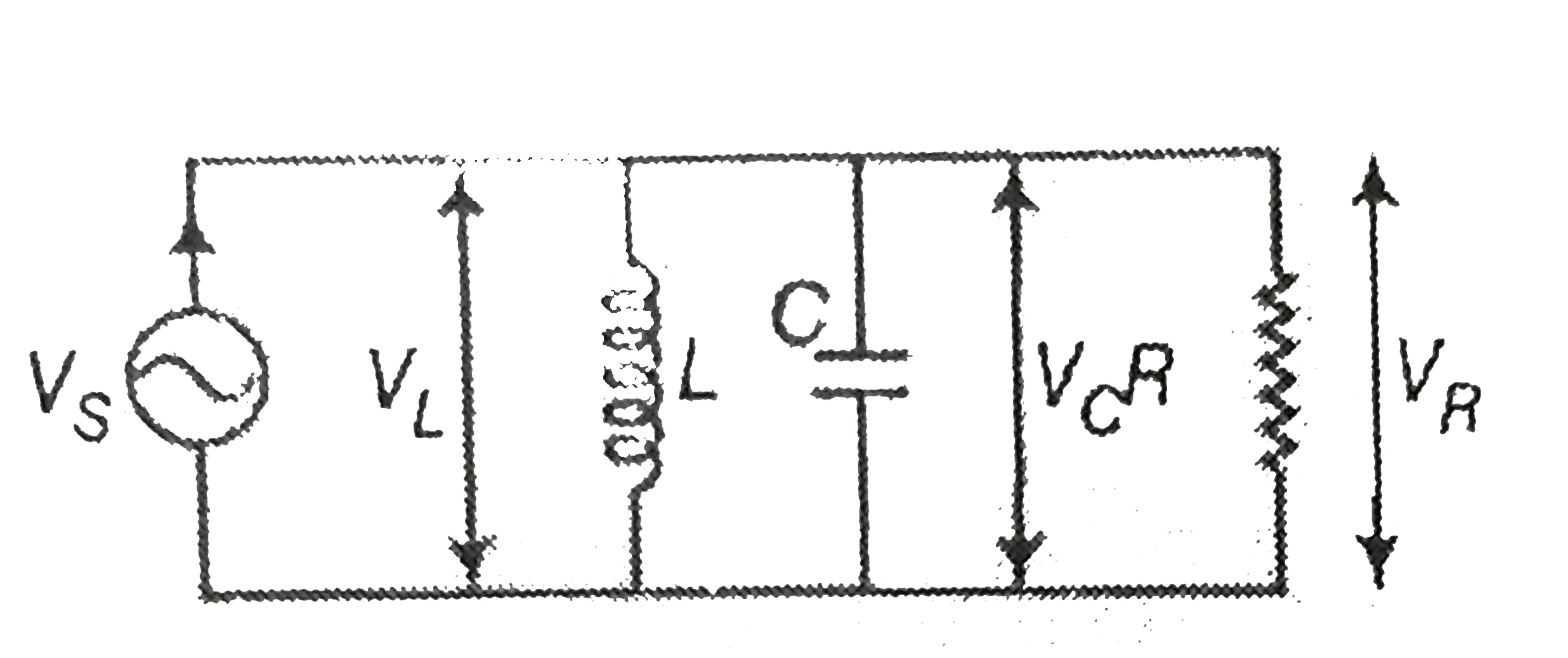View SolutionWhen perssure is increase at constant temperature, volume of gas decreases, AB → gases,Bc → vapour +liquid ,CD → liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
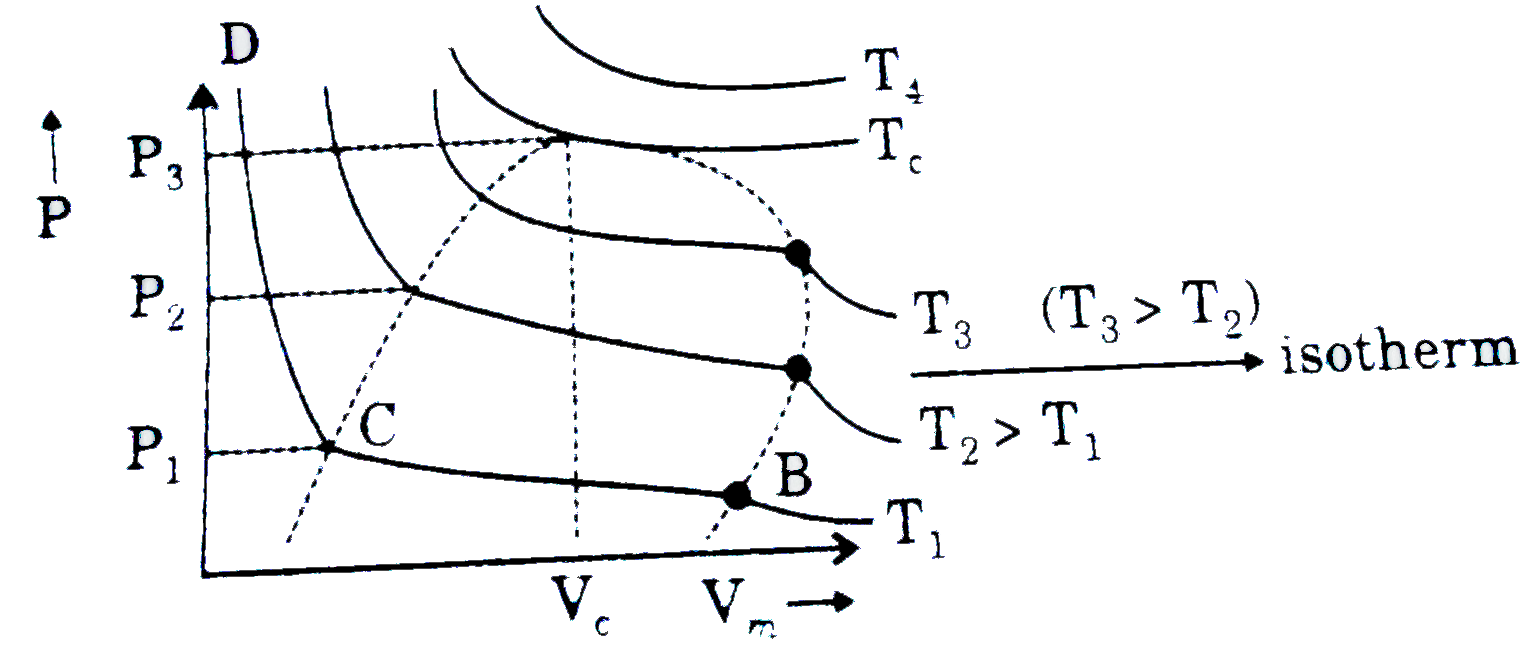
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
A scientist proposed the following equation of state
P=RTVm−BV2m+CV2m If this equation leads to the critical behaviour then critical temperature isView SolutionWhen perssure is increase at constant temperature, volume of gas decreases, AB → gases,Bc → vapour + liquid ,CD →liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
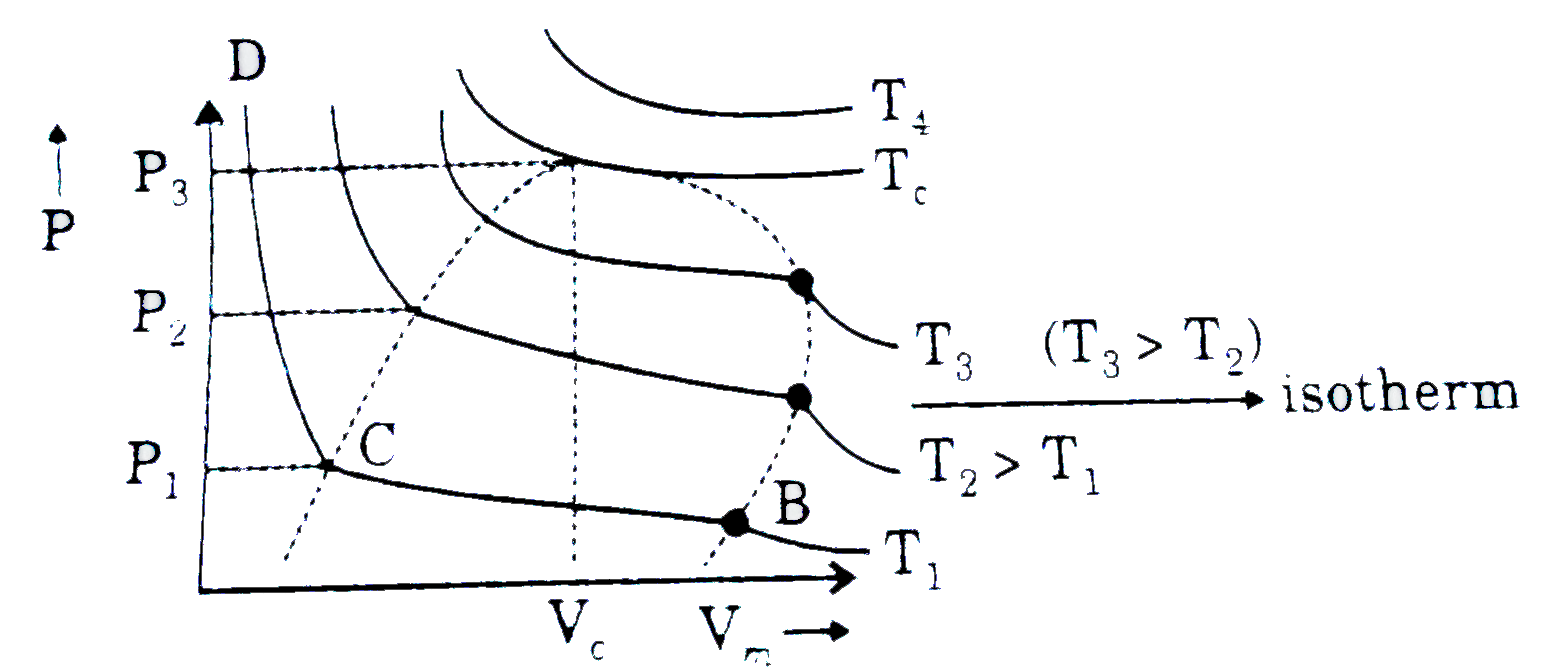
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
If the critical constants for a hypothetical van der Waals' gas are Vc=150cm2mol−1,pc=300K Then the approxomate radius of the molecule is :
(TakeR=112Latmmol−1K−1]View SolutionWhen perssure is increase at constant temperature, volume of gas decreases, AB → gases,BC → vapour +liquid ,CD → liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
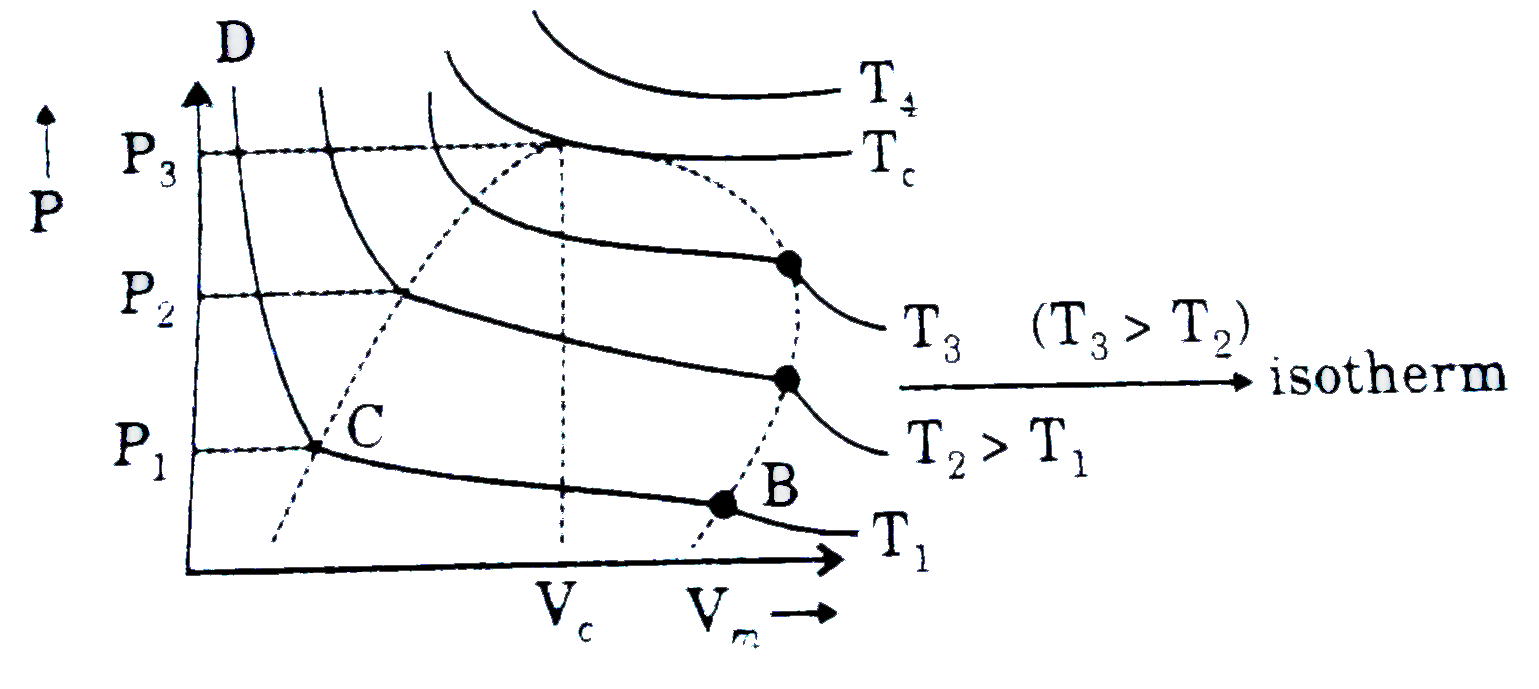
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
Identify the wrong statement related to the following graph
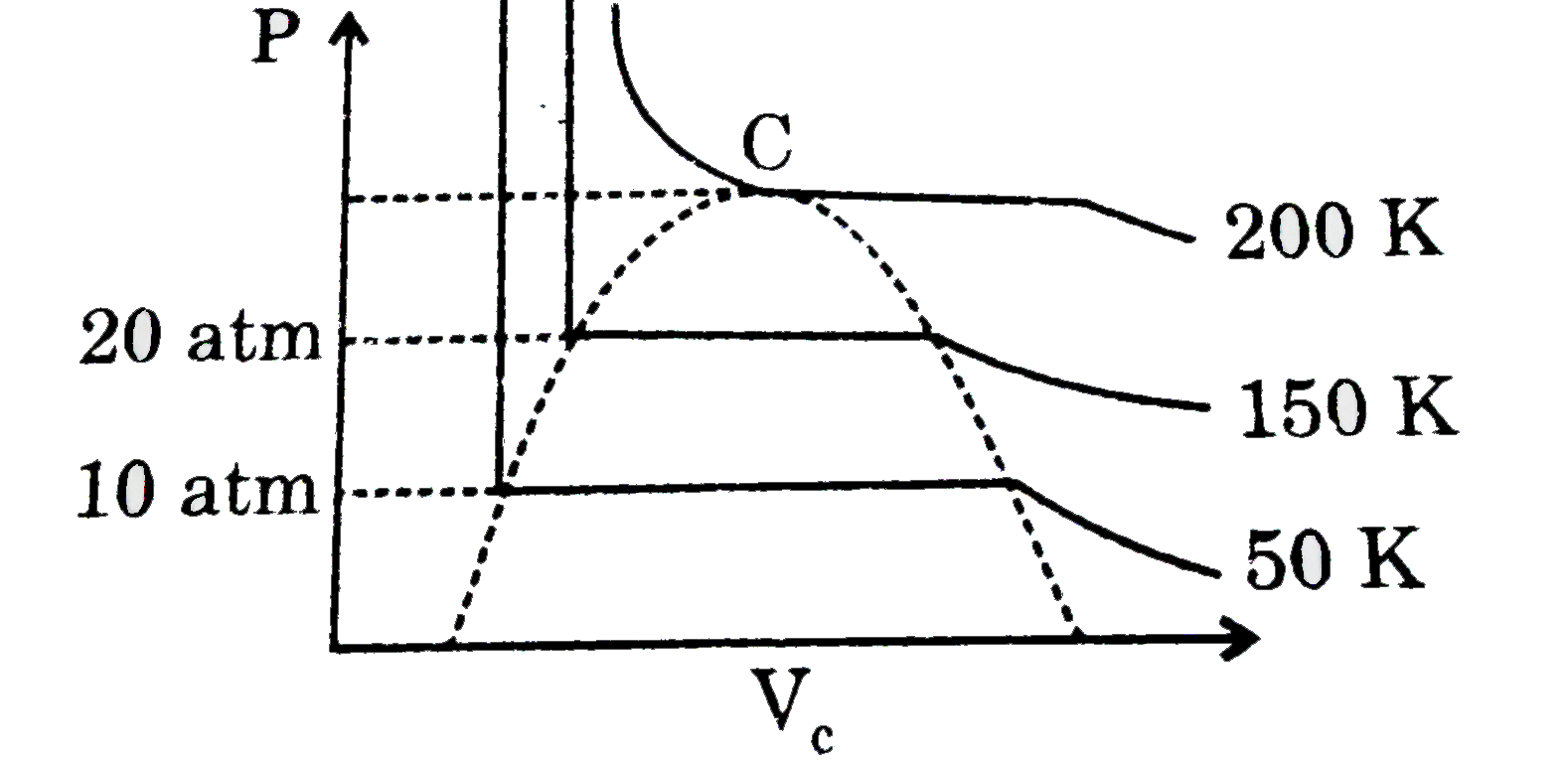View Solution