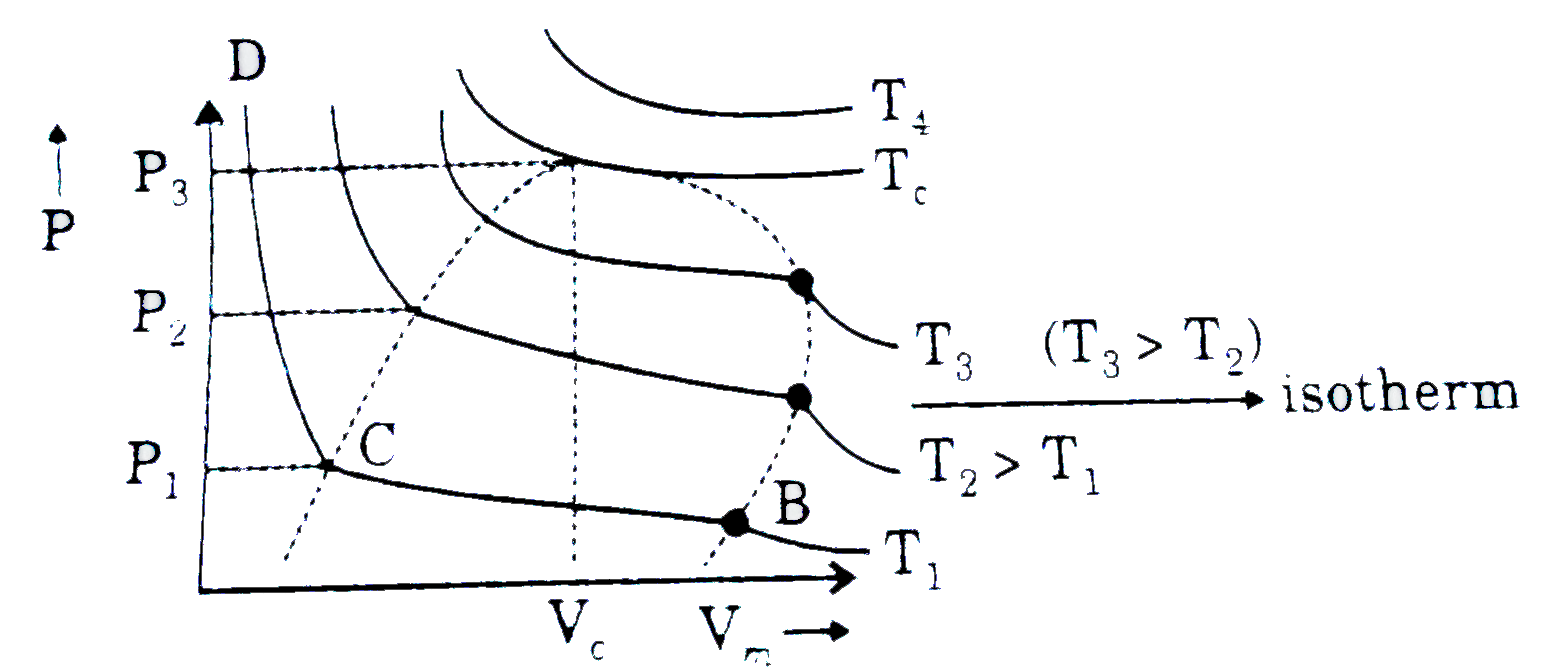
When perssure is increase at constant temperature, volume of gas decreases, AB $\to$ gases,Bc $\to$ vapour + liquid ,CD $\to$ liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
$T_{e}$ or critical temp : Temperature above which a gas can not be liquified
$V_{e}$ or critical volume : Volume occupied by one mole of gas at $T_{e}$ abd $P_{e} .$

Critical constant Using van der Waals' Equations
$(P + \frac{a}{V_{m}^{2}}) (V_{m} - b) = R T$
$\Rightarrow (P V_{m}^{2} + a) (V_{m} - b) = R T V_{m}^{2}$
$P V_{m}^{3} + a V_{m} - P b V_{m}^{2} = a b - R T V_{m}^{2} = 0$
$\Rightarrow V_{m}^{3} - V_{m}^{2} (b + \frac{R T_{e}}{P}) + \frac{a}{p} \frac{V}{m} - \frac{a b}{p} = 0$
Since equation is cubic in $V_{m}$ hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
$V_{m}^{3} - V_{m}^{2} (b + \frac{R T_{c}}{P_{c}}) + \frac{a}{p_{c}} V_{m} - \frac{a b}{p_{c}} = 0 ... . (i)$
But at critical point all three roots of the equation should be equal, hence equation should be :
$V_{m} = V_{c}$
${(V_{m} - V_{c})}_{m}^{3} = 0$
$V_{m} - 3 V_{m}^{2} V_{c} + 3 V_{m} V_{c}^{2} - V_{c}^{3} = 0$ ....(ii)
Comparing with equation (i)
$b + \frac{R T_{c}}{p_{c}} = 3 V_{c}$ ...(iii)
$\frac{a}{p_{c}} = 3 V_{e}^{2}$ ...(iv)
$\frac{a b}{p_{c}} = V_{c}^{3}$ ....(v)
from eqns.(iv) and (v0, $V_{c} = 3 b$
from eq. (iv) $p_{c} = \frac{a}{3 V_{c}^{2}}$ substituting $p_{c} = \frac{a}{3 {(3 b)}^{2}} = \frac{a}{27 b^{2}}$
from e.q (iii) $\frac{R T_{c}}{p_{c}} = 3 V_{c} - b = 9 b - b = 8 b$
$\Rightarrow T_{c} = \frac{8 a}{27 R b}$
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
${(\frac{\partial P}{\partial V_{m}})}_{T c} = 0$ ...(iv)
$\frac{\partial}{\partial V_{m}} {(\frac{\partial P}{\partial V_{m}})}_{T c} = 0$
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two $T_{c} P_{c}$ and $V_{c}$ can be calculated
If the critical constants for a hypothetical van der Waals' gas are $V_{c} = 150 c m^{2} m o l^{- 1}, p_{c} = 300 K$ Then the approxomate radius of the molecule is :
$(Take R = \frac{1}{12} L a t m m o l^{- 1} K^{- 1}]$

A

${(\frac{75}{2 π N_{A}})}^{1 / 3}$

B

${(\frac{75}{8 π N_{A}})}^{1 / 3}$

C

${(\frac{3}{π N_{A}})}^{1 / 3}$

D

${(\frac{3}{256 π N_{A}})}^{1 / 3}$

Text Solution

Verified by Experts

The correct Answer is:B

|

Updated on:21/07/2023

Class 12 CHEMISTRY GRAPHICAL INTERPRETATION

Topper's Solved these Questions

Similar Questions

GRB PUBLICATION-GRAPHICAL INTERPRETATION-Comprehension

Home
Ask Doubt
Profile