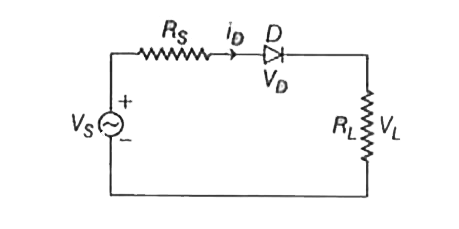
In the diode-based rectifier circuit given below, if Vs=Vmsinωt and the diode is ideal, then the average value of VL is
RL(RL+RS)Vmπ
RLVmsinωt
RL(RL+RS)Vm
RL(RL+RS)Vmsinωt
The correct Answer is:A
Given, AC voltage, Vs=VmsinωtandVm= maximum value of voltage In the given circuit diode will only conduct current in forward bias, so output across RI, will be
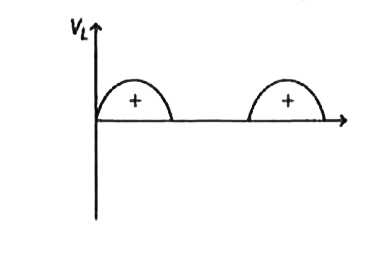
Average voltage,Vav=Vmπ
average current Iav=VavR
Toal resistance, R=Rs+RL
Lav=Vm(RS+RL)π
Now, voltage across RL,
VL=Iav.RL
VL=RLRS+RL.Vmπ
Topper's Solved these Questions
Similar Questions
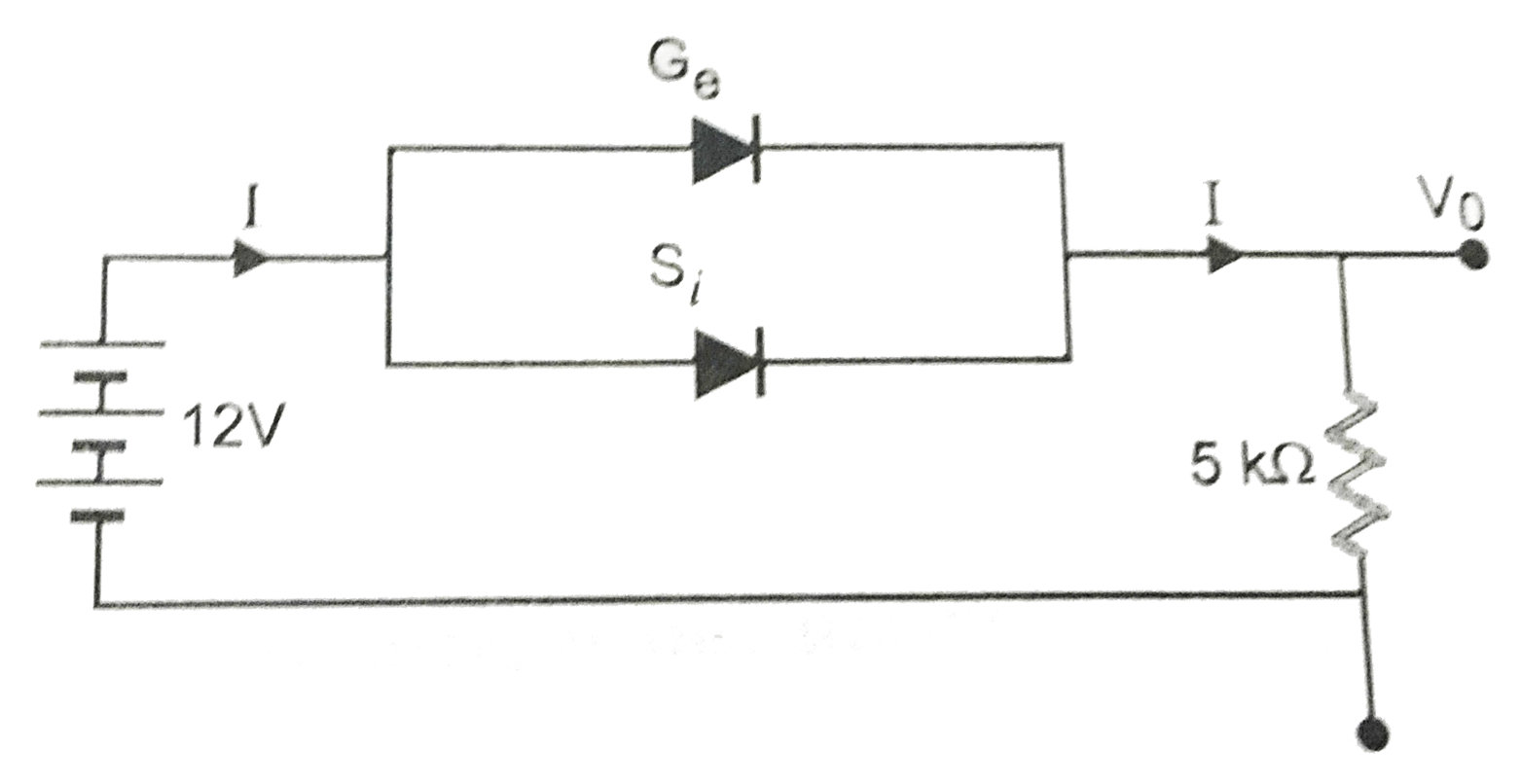
Calculate the value of output voltageV0 and I if the Si diode and the Ge diode conduct at 0.7 V and 0.3V respectively, in the circuit given in Fig. If now Ge diode connections are reversed, what will be the new values of V0 and I.
View SolutionIn a full wave rectifiers in which input voltage is represented by V=VMsinωt, then peak inversion voltage of non-conducting diode will be
View Solution
Knowledge Check
For an ac circuit V=15sinωt and I=20cosωt the average power consumed in this circuit is
A300 wattB150 wattC75 wattDzeroIn a full wave rectifiers in which input voltage is represented by V=VMsinωt, then peak inversion voltage of non-conducting diode will be
A−VMBVM/2C2VMD0In a series L.C.R. circuit alternating emf (v) and current (i) are given by the equation v=v0sinωt, i=i0sin(ωt+π3) The average power dissipated in the circuit over a cycle of AC is
Av0I02Bv0I04C√32v0I0Dzero
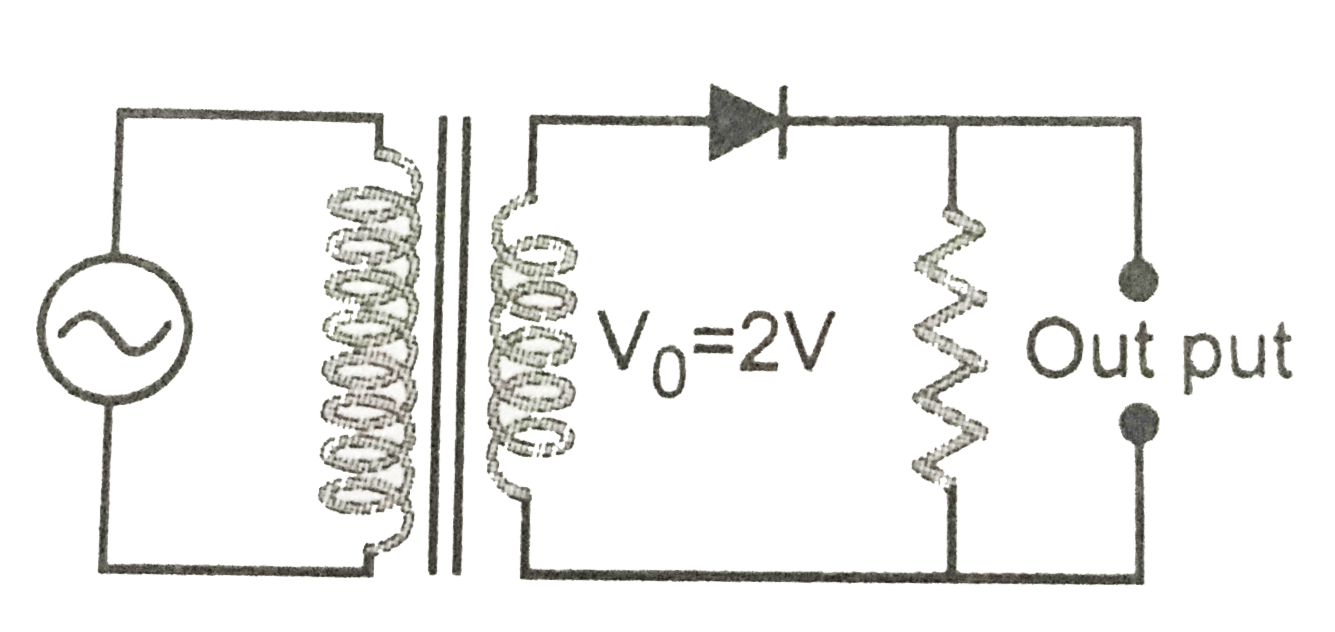
Consider the half wave rectifier circuit Fig.Assume the diode to be a silicon diode with a thershold voltage of 0.7V. Draw the output if the input is a sine wave with an amplitude of 2V.
View SolutionThe voltage over a cycle varies as
V=V0sinωt for 0≤t≤πω
=−V0sinωt for πω≤t≤2πω
The average value of the voltage one cycle is
View SolutionThe velocity of a particle is given by v=v0sinωt, where v0 is constant and ω=2π/T. Find the average velocity in time interval t=0to t=T/2.
View SolutionThe voltage over a cycle varies as
V=V0sinωt for 0≤t≤πω
=−V0sinωt for πω≤t≤2πω
The average value of the voltage one cycle is
View SolutionThe voltage over a cycle varies as
V=V0sinωt for 0≤t≤πω
=−V0sinωt for πω≤t≤2πω
The average value of the voltage one cycle is
View Solution
