Figure 27-12 shows a circuit whose elements have the following values: ε1=3.0V,ε2=6.0V,R1=2.0ΩR2=2.0Ω. The three batteries are ideal batteries. Find the magnitude and direction of the current in each of the three branches
It is not worthwhile to try to simplify this circuit, because no two resistors are in parallel, and the resistors that are in series (those in the right branch or those in the left branch) present no problem. So, our plan is to apply the junction and loop rules.
Junction rule: Using arbitrarily chosen directions for the currents as shown in Fig. 27-12, we apply the junction rule at point a by writing
i3=i1+i2
An application of the junction rule al junction b gives only the same equation, so we next apply the loop rule to any two of the three loops of the circuit.
Left-hand loop: We first arbitrarily choose the left-hand loop, arbitrarily start at point b, and arbitrarily traverse the loop in the clockwise direction, obtaining
−i1R1+ε1−i1R1−(i1+i2)R2−ε2=0
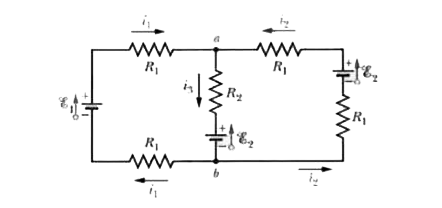
Figure 27-12 A maltiloop circuit with three ideal batteries and five resistances.
where we have used (i1+i2) instead of i3 in the middle branch. Substituting the given data and simplifying yeild
i1(8.0Ω)+i2(4.0Ω)=−3.0V
Right-hand loop: For our second application of the loop rule, we arbitrarily choose to traverse the right-hand loop counterclockwise from point b, finding
−i2R1+ε2−i2R1−(i1+i2)R2−ε2=0
Substituting the given data and simplifying yield
i1(4.0Ω)+i2(8.0Ω)=0
Combining equations: We now have system of two equations (Eqs. 27-27 and 27-28) in two unknowns (i1,andi2) to solve either "by hand” (which is easy enough here) or with a "math package." (given in Appendix E.) We find i1=−0.50A
(The minus sign signals that our arbitrary choice of direction for i1 in Fig. 27-12 is wrong, but we must wait to correct it.) Substituting i1=−0.50A into Eq. 27-28 and solving for i2, then give us i2=0.25A. With Eq. 27-26 we then find that i3=i1+i2=−0.50A+0.25A
The positive answer we obtained for i2 signals that our choice of direction for that current is correct. However. the negative answers fort, and indicate that cour choices for those currents are wrong. Thus, as a last ster here, we correct the answers by reversing the arrows for and in Fig, 27-12 and then writing. 20.50 and
i1=0.50Aandi3=0.25A
Caution: Always make any such correction as the last step and not before valeulaling at the currents.
Topper's Solved these Questions
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Checkpoints
7 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Problems
45 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
Similar Questions
Figure shows a circuit with three ideal batteries in it. The circuit elements h ave the following values
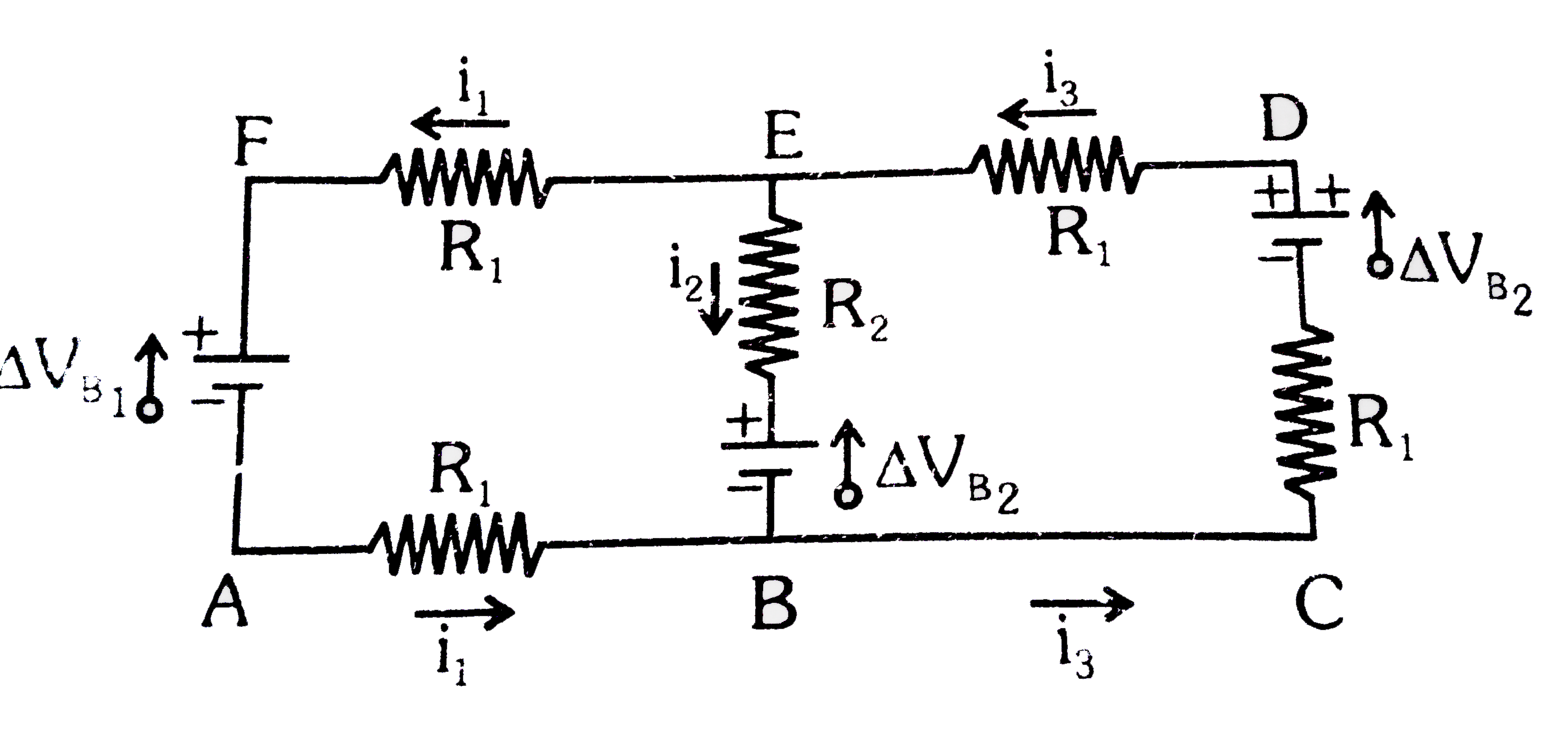
ΔVB1=3.0V,ΔVB2=6.0V
R1=2.0Ω,R2=4.0Ω The currents i1,i2 and i3 as shown in the circuit have the values.
View SolutionIn Fig. 27-9, what is the potential difference V.d−Vc between points d and c if ε1=4.0V.ε2−1.0V,R1=R2=10Ω,andR3=8.0Ω, and the battery is ideal?
View Solution
Knowledge Check
Figure shows a circuit with three ideal batteries in it. The circuit elements h ave the following values
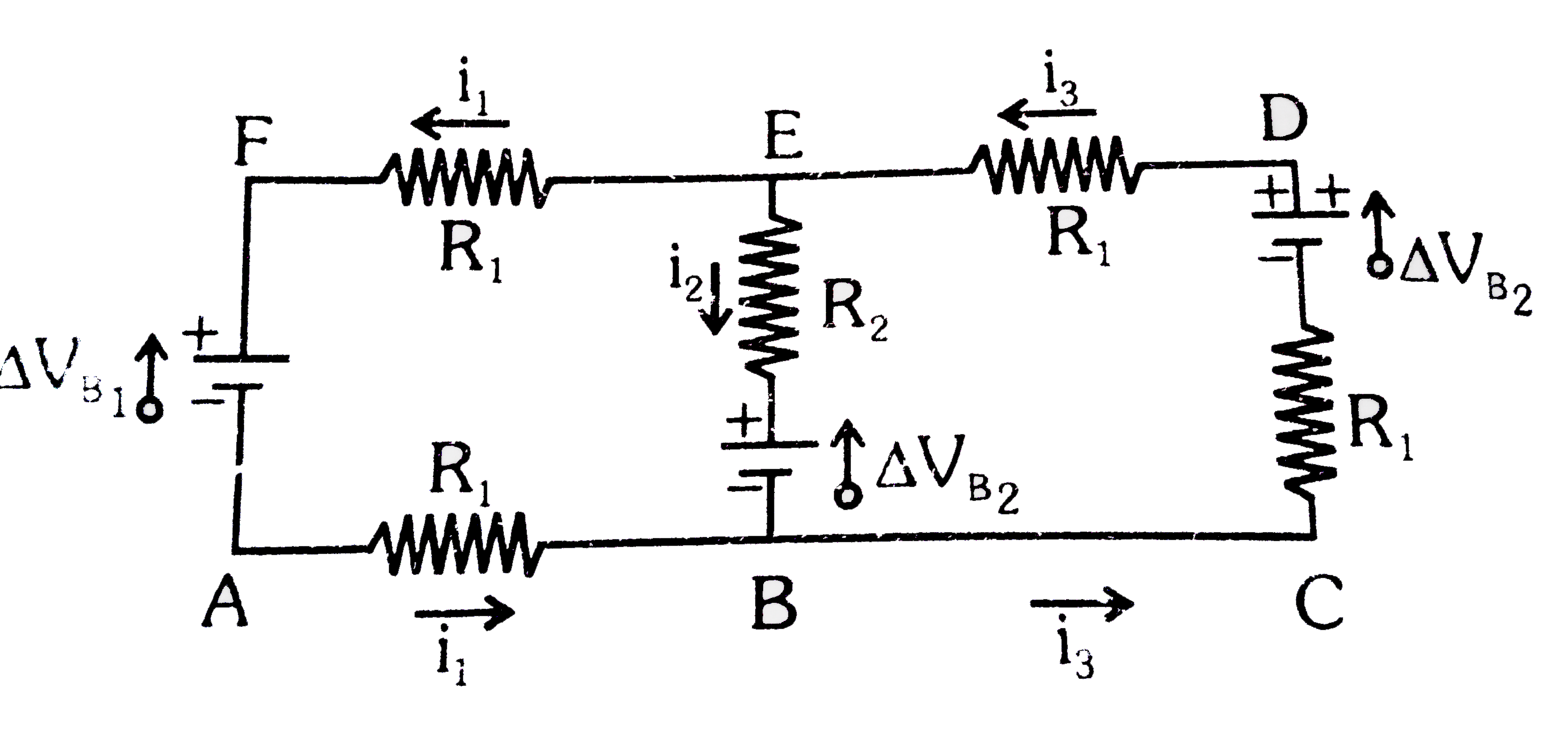
ΔVB1=3.0V,ΔVB2=6.0V
R1=2.0Ω,R2=4.0Ω The currents i1,i2 and i3 as shown in the circuit have the values.A0.50A,-0.25A,+0.25AB0.25A,-0.50A,-0.25AC0.50A,0.50A,1.0AD−0.25A,0.50A,0.25AIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
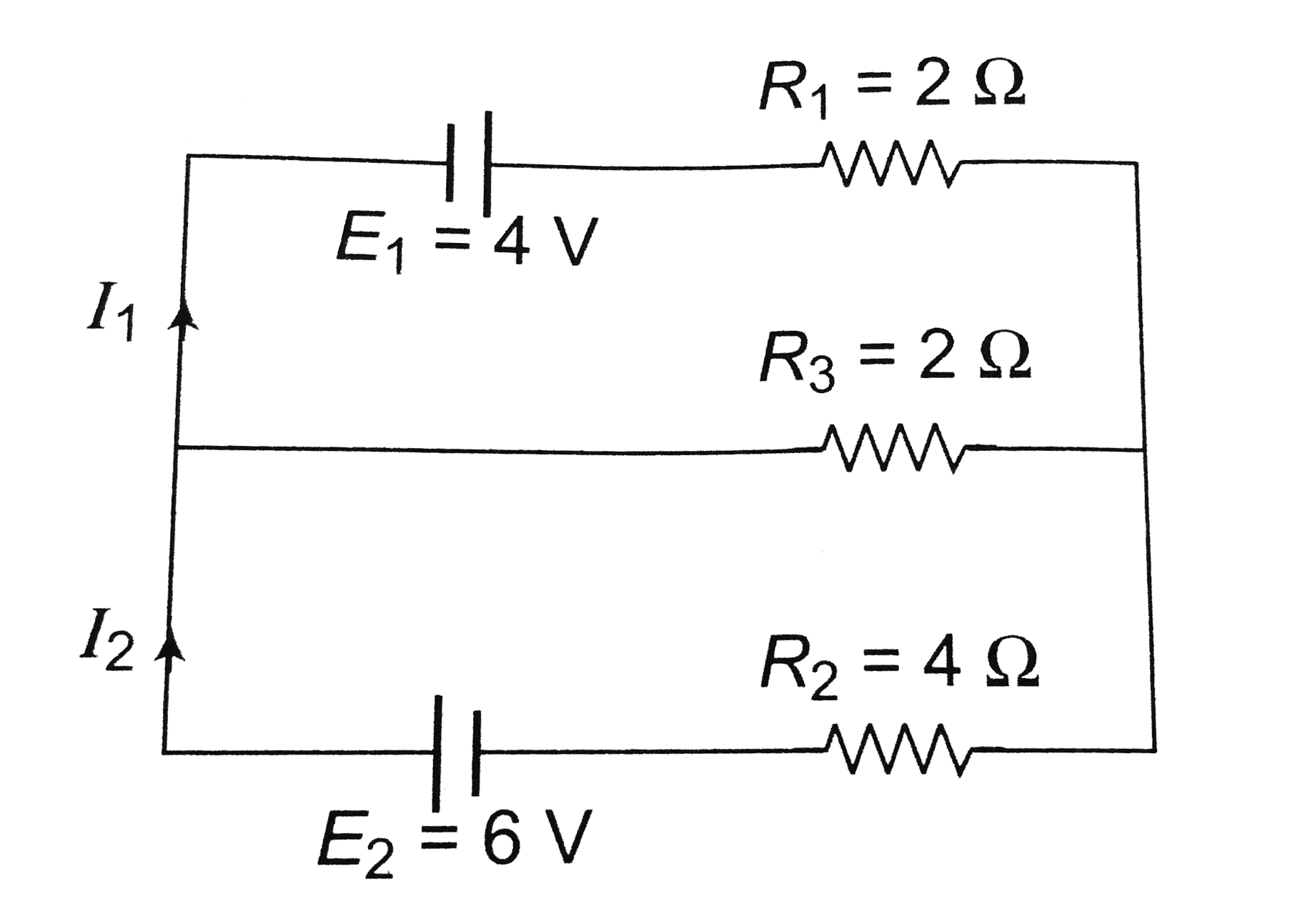 A1.6AB1.8AC1.25AD1.0A
A1.6AB1.8AC1.25AD1.0A
The emf and resistances in the circuit of Fig 27-8a have the following values:
ε1=4.4V.ε2=2.1V,
r1=2.3Ω,r2=1.8Ω,R=5.5Ω
(a) What is the current I in the circuit?
(b) What is the potential difference between the terminals of battery 1 in Fig. 27 8a?
View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is

View SolutionIn the following circuit ,E1=4V,R1=2Ω,
E2=6V,R2=2Ω,andR3=4Ω. Find the currents i1andi2
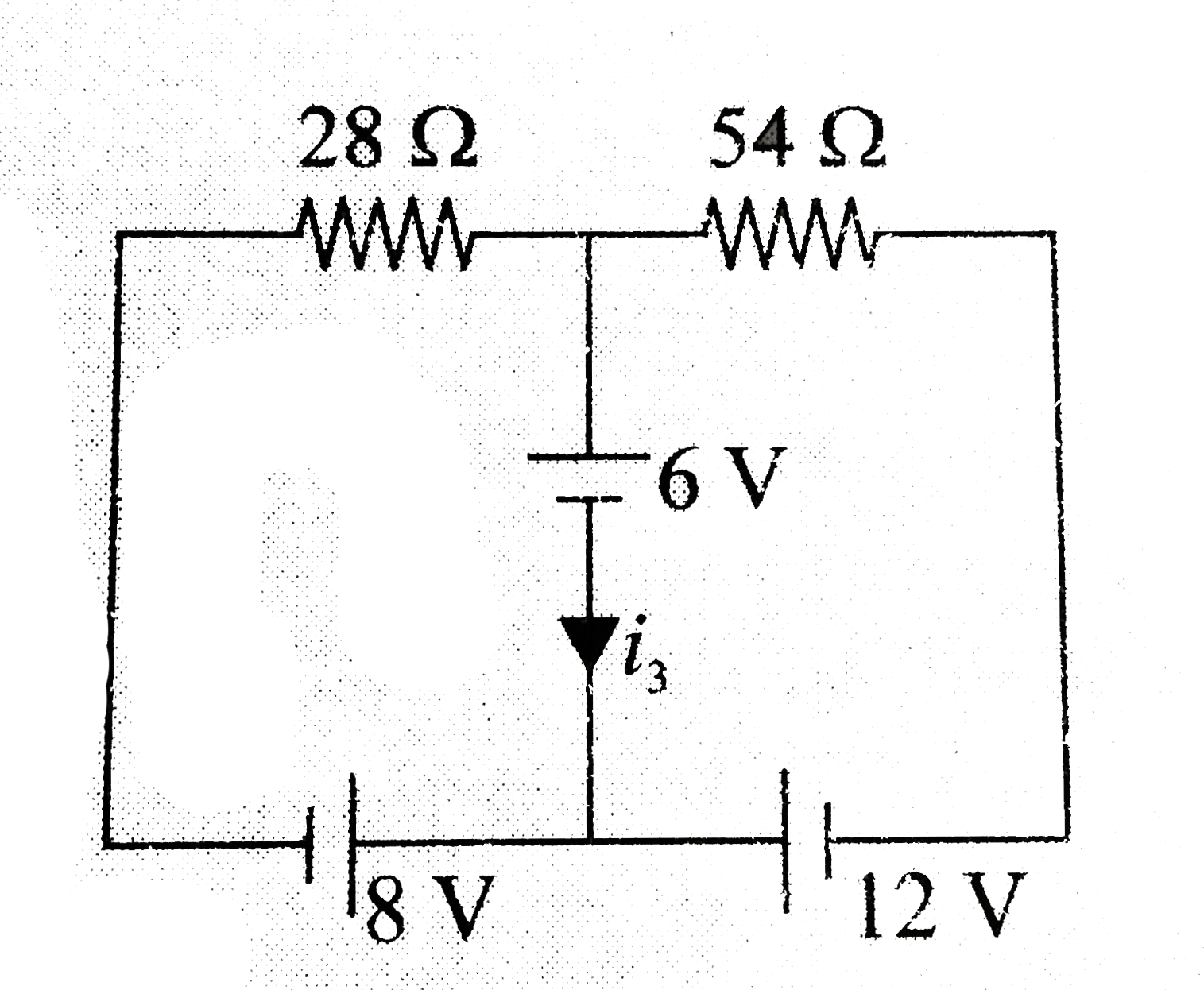
View SolutionIn the following circuit ,E1=4V,R1=2Ω,
E2=6V,R2=2Oemga,andR3=4Ω. Find the currents i1andi2
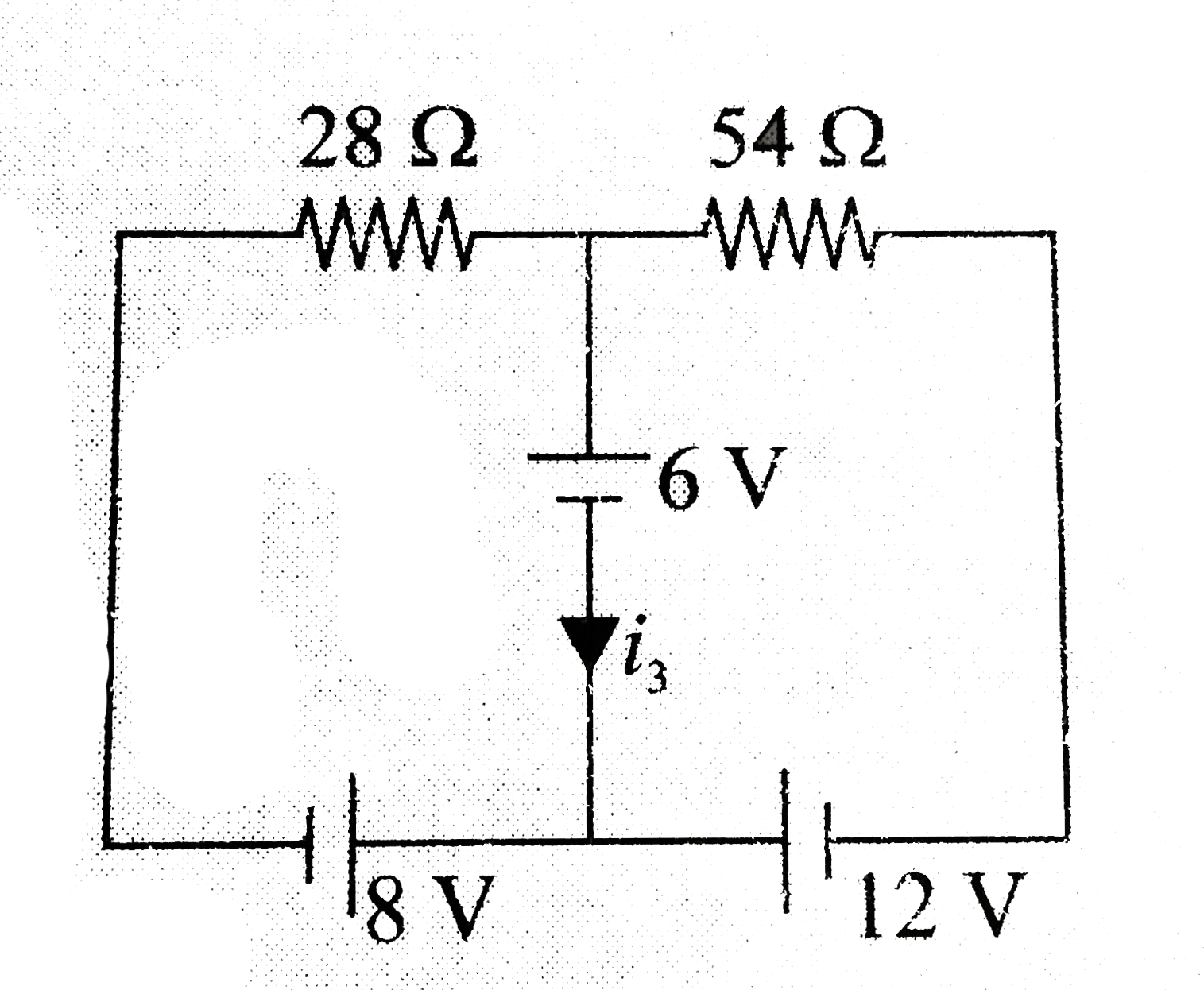
View SolutionFigure 27-11a shows a multiloop circuit containing one ideal battery and four resistances with the following values:
R1=20Ω,R2=20Ω,ε=12V,
R3=30Ω,R4=8.0Ω
(a) What is the current through the battery?
(b) What is the current i2 through R2?
(c) What is the current i3 through R3?
View SolutionIn the circuit shown in figure
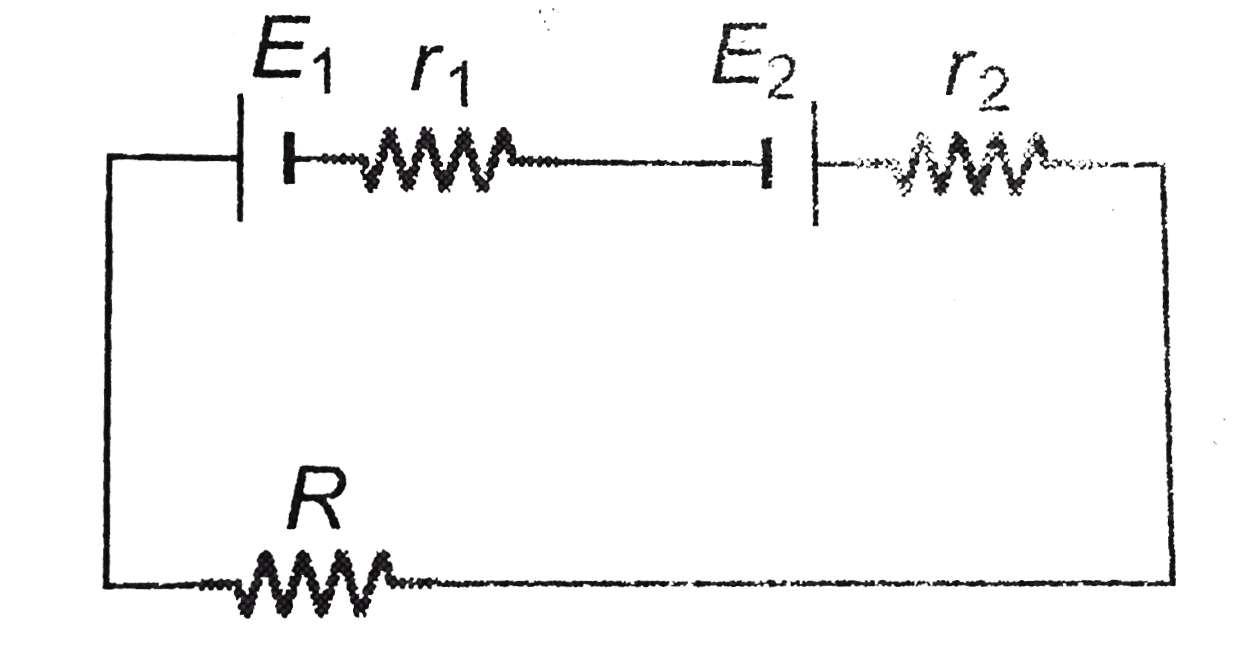
E1=10V,E2=4V,r1=r2=1Ω and R=2Ω.
Find the potential difference across battery 1 and battery 2.
View Solution
