A metallic wire with resistance λ per unit length is bent to form α circle of radius R. Calculate the effective resistance between the effective resistance between the points P and Q , making an angle of 90∘ with each other at the centre.

Text Solution
Let R1 =Resistance of part PMQ
R2= Resistance of part of PQ.
Circumference of circle =2πR (Here, R is the radius of circle).
If λ= resistance per unit length, then
R1=34×2πRλ
R2=14×2πRλ
As the resistance are connected in parallel the resultant resistance will be given by
R=R1R2R1+R2=34(2πR)λ×14(2πR)λ34(2πR)λ+14(2πR)λ
=316λ2(2πR)22πRλ
=332λ(2πR)
=316λπR

|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE PROBLEMS
71 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
What is the effective resistance between points P and Q?
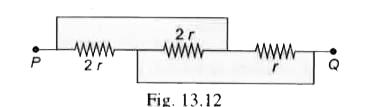 Ar2Br3C2R3D4r3
Ar2Br3C2R3D4r3What is the effective resistance between points P and Q?
 A5ΩB10ΩC15ΩD20Ω
A5ΩB10ΩC15ΩD20ΩThe effective resistance between P and Q in the given circuit is
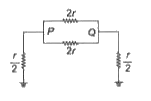 A3r2B3rC2rDr2
A3r2B3rC2rDr2
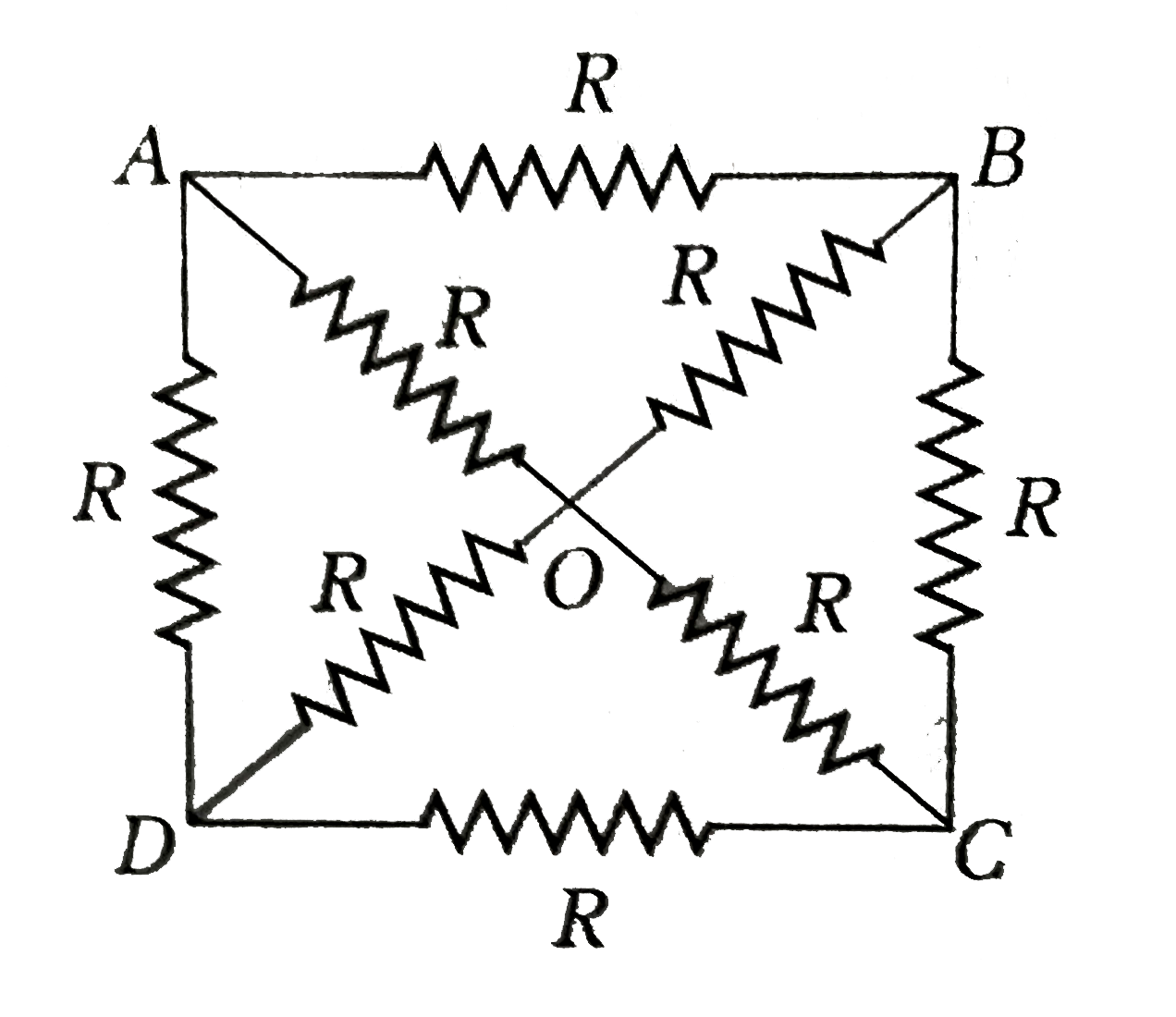
The effective resistance between points A and C for the network shown figure is
View SolutionThe effective resistance between P and Q for the following network is
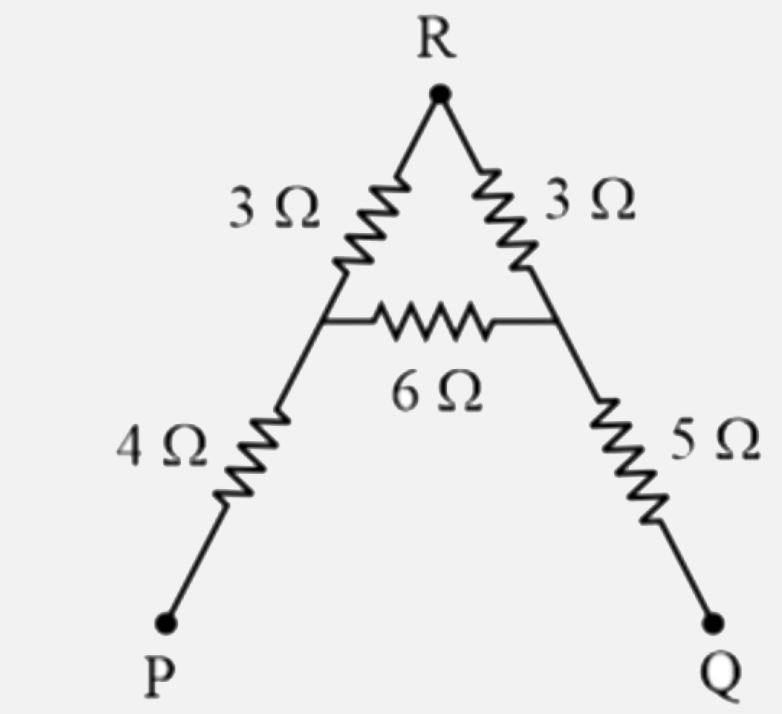
View SolutionThe effective resistance between P and Q for the following network is

View SolutionThe effective resistance between p and q in given figure is

View SolutionThe effective resistance between points P and Q of the electrical circuit shown in the figure is
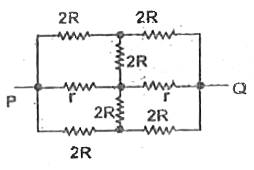
View Solution