How many time constants will elapse before a capacitor gains 99% of its steady state charge?
1
9.2
4.6
18.4
The correct Answer is:C
To determine how many time constants will elapse before a capacitor gains 99% of its steady state charge, we can follow these steps:
Step 1: Understand the charging equation of a capacitor
The charge Q on a capacitor at any time t during charging can be expressed using the formula:
Q=Q0(1−e−tτ)
where:
- Q0 is the maximum charge (steady state charge),
- τ is the time constant of the circuit.
Step 2: Set up the equation for 99% charge
We want to find the time t when the capacitor reaches 99% of its steady state charge. Therefore, we set:
Q=0.99Q0
Step 3: Substitute into the charging equation
Substituting Q into the charging equation gives:
0.99Q0=Q0(1−e−tτ)
Step 4: Simplify the equation
We can cancel Q0 from both sides (assuming Q0≠0):
0.99=1−e−tτ
Rearranging this gives:
e−tτ=1−0.99=0.01
Step 5: Take the natural logarithm of both sides
Taking the natural logarithm (ln) of both sides results in:
−tτ=ln(0.01)
Step 6: Solve for t
We know that ln(0.01)=ln(1100)=−ln(100). Thus:
−tτ=−ln(100)
This simplifies to:
tτ=ln(100)
Step 7: Calculate ln(100)
Using the property of logarithms:
ln(100)=ln(102)=2ln(10)≈2×2.3=4.6
Thus, we have:
tτ=4.6
Step 8: Conclusion
This means that the time t taken to reach 99% of the steady state charge is approximately 4.6τ. Therefore, the answer is:
4.6 time constants
The charge Q on a capacitor at any time t during charging can be expressed using the formula:
Q=Q0(1−e−tτ)
where:
- Q0 is the maximum charge (steady state charge),
- τ is the time constant of the circuit.
We want to find the time t when the capacitor reaches 99% of its steady state charge. Therefore, we set:
Q=0.99Q0
Substituting Q into the charging equation gives:
0.99Q0=Q0(1−e−tτ)
We can cancel Q0 from both sides (assuming Q0≠0):
0.99=1−e−tτ
Rearranging this gives:
e−tτ=1−0.99=0.01
Taking the natural logarithm (ln) of both sides results in:
−tτ=ln(0.01)
We know that ln(0.01)=ln(1100)=−ln(100). Thus:
−tτ=−ln(100)
This simplifies to:
tτ=ln(100)
Using the property of logarithms:
ln(100)=ln(102)=2ln(10)≈2×2.3=4.6
Thus, we have:
tτ=4.6
This means that the time t taken to reach 99% of the steady state charge is approximately 4.6τ. Therefore, the answer is:
4.6 time constants
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION FOR COMPETITIVE EXAMINATIONS)20videos
CURRENT ELECTRICITY
- BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)45videos
CURRENT ELECTRICITY
- BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (NUMERICAL PROBLEMS)24videos
CURRENT ELECTRICITY
- BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test16videos
ATOMS
- BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST15videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
How many time constans will elapse before a fully charged capacitor loses 99% of its stored charge when connected across a resistor?
A1B9.2C4.6D18.4 - Question 2 - Select One
Calculate charge on capacitor in steady state.
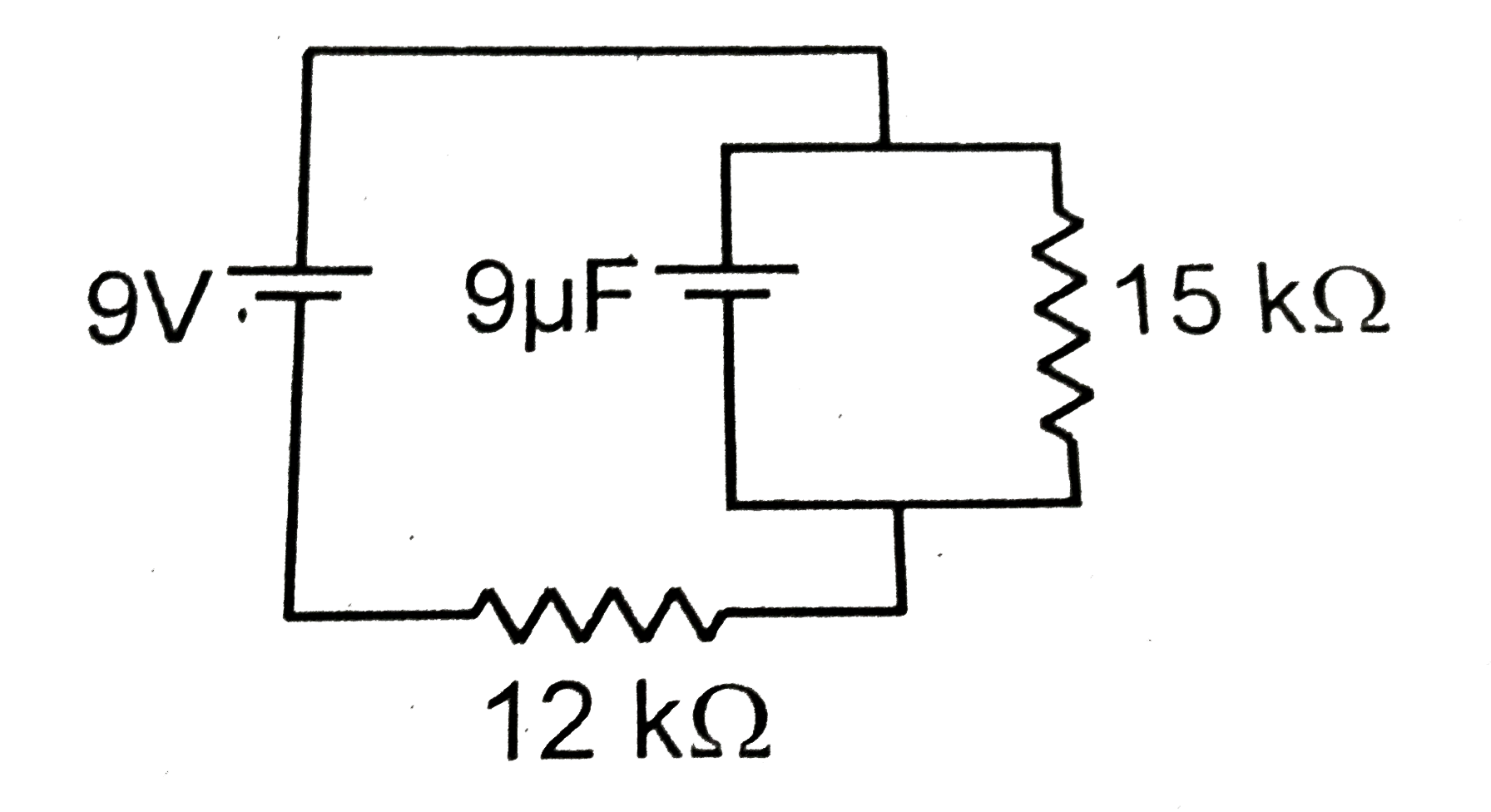 A20μCB30μCC45μCD60μC
A20μCB30μCC45μCD60μC
How many time constants will elapse before the current in a charging RC circuit drops to half of its initial value?Answer the same question for a discharging RC circuit.
View SolutionHow many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging RC circuit ?
View SolutionHow many time constant will elapse before the power delivrered by the battery drops to half of its maximum value.
View Solutionhow many time constants will elapse before the power delovered by the battery drops to half of its maximum value in an RC circuit ?
View SolutionFind the charge on capacitor in steady state.
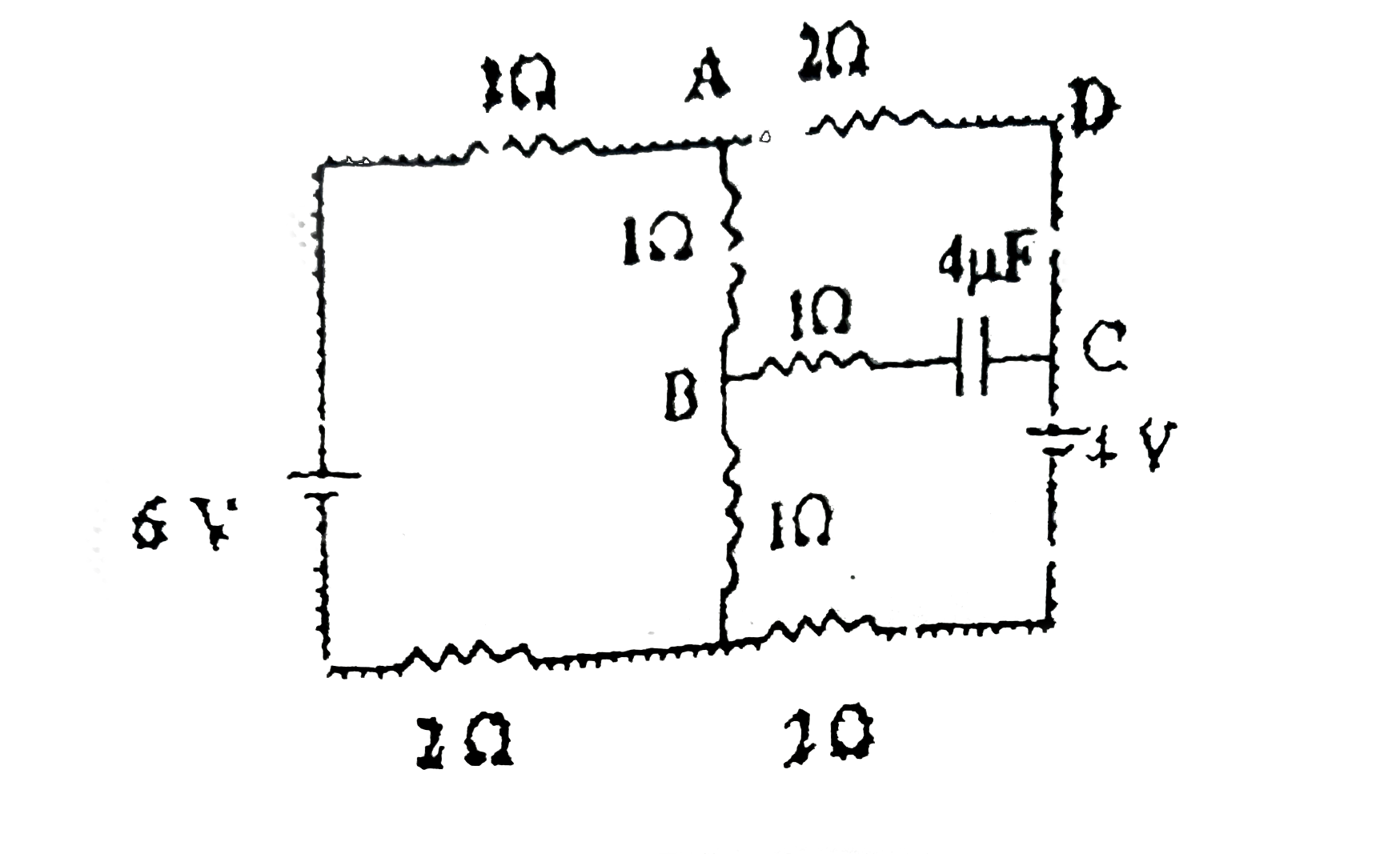 View Solution
View SolutionThe charge on the 4μF capacitor in the steady state is
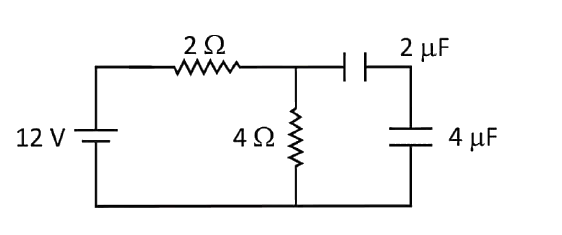 View Solution
View Solution

