One ideal cell is used to drive current in a metre bridge circuit. In an experiment x is the balancing length obtained. If we replace the wire of the metre bridge with another wire of material having more rsistivity and lesser diameter, the new balancing length will be
less than x
more than x
equal to x
more or less that depends on the ratio of resistances used in the left and right gap of metre bridge.
The correct Answer is:C
To solve the problem, we need to analyze how the balancing length in a meter bridge circuit is affected when we replace the wire with another wire that has higher resistivity and a smaller diameter.
1. Understanding the Meter Bridge:
The meter bridge consists of a wire of uniform cross-section and length 1 meter. When a current is passed through it, a galvanometer is used to find the balancing point (null point) where the potential difference across the two segments of the wire is equal.
2. Initial Balancing Condition:
Let the initial balancing length be x. According to the principle of the meter bridge, we have:
xL−x=R1R2
where L=100cm (the total length of the wire), R1 is the resistance in one arm, and R2 is the resistance in the other arm.
3. Replacing the Wire:
When we replace the wire with another wire that has higher resistivity (ρ′>ρ) and a smaller diameter, the resistance of the new wire will increase. The resistance of a wire is given by:
R=ρLA
where A is the cross-sectional area of the wire. A smaller diameter means a smaller area, which increases the resistance.
4. Effect on Balancing Length:
The new resistance R′ can be expressed as:
R′=ρ′LA′
Since R1 and R2 are constant (not changing), the new balancing length x′ will still satisfy the meter bridge equation:
x′L−x′=R1R2
This implies that the ratio x′L−x′ remains the same as xL−x.
5. Conclusion:
Since the ratio of the resistances R1 and R2 does not change, the new balancing length x′ will remain equal to the original balancing length x. Thus, we conclude:
x′=x
Final Answer:
The new balancing length will be equal to x.
---
The meter bridge consists of a wire of uniform cross-section and length 1 meter. When a current is passed through it, a galvanometer is used to find the balancing point (null point) where the potential difference across the two segments of the wire is equal.
Let the initial balancing length be x. According to the principle of the meter bridge, we have:
xL−x=R1R2
where L=100cm (the total length of the wire), R1 is the resistance in one arm, and R2 is the resistance in the other arm.
When we replace the wire with another wire that has higher resistivity (ρ′>ρ) and a smaller diameter, the resistance of the new wire will increase. The resistance of a wire is given by:
R=ρLA
where A is the cross-sectional area of the wire. A smaller diameter means a smaller area, which increases the resistance.
The new resistance R′ can be expressed as:
R′=ρ′LA′
Since R1 and R2 are constant (not changing), the new balancing length x′ will still satisfy the meter bridge equation:
x′L−x′=R1R2
This implies that the ratio x′L−x′ remains the same as xL−x.
Since the ratio of the resistances R1 and R2 does not change, the new balancing length x′ will remain equal to the original balancing length x. Thus, we conclude:
x′=x
The new balancing length will be equal to x.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION FOR COMPETITIVE EXAMINATIONS)20videos
CURRENT ELECTRICITY
- BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)45videos
CURRENT ELECTRICITY
- BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (NUMERICAL PROBLEMS)24videos
CURRENT ELECTRICITY
- BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test16videos
ATOMS
- BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST15videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
If in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimeter is
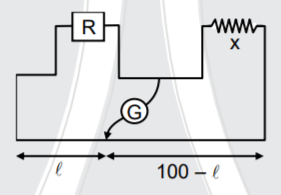 View Solution
View SolutionIn an experiment on metre bridge the balancing length on wire is 'l'. What would be its value, if the radius of the metre bridge wire is doubled ? Justify your answer.
View Solution
Knowledge Check
- Question 1 - Select One
In a metre bridge experiment lx and lr are the balancing lengths and R is known resistance then unkown, resistance is given by
AX=lxlr.RBX=Rlx.lrCX=lx.lr.RDX=l2xR - Question 2 - Select One
A mete bridge is used to determine the resistance of an unknown wire by measuring the balance point length l. If the wire is replaced by another wire of same material but with double the length and half the thickness the balancing point is expected to be
A18lB14lC8lD16l - Question 3 - Select One
In a metre bridge experiment, the balancing length from the left end is found to be 20 cm. If a standard resistance of 20 ohm is kept in the right gap, then the value of the unknown resistance in the left gap is
A5ΩB10ΩC15ΩD7.5Ω
Explain : In Wheatstone's metre bridge experiment, the null point is obtained in the middle one-third of the wire.
View SolutionIn a metre bridge the length of the wire is 100 cm. At what point will the balance point be obtained if the two resistances are in the ratio of 4:5.
View SolutionIn a metre bridge, the length of the wire is 100 cm. At what position will the balance point be obtained if the two resistances are in the ratio 2 : 3?
View SolutionIn metre bridge experiment, with a standard resistance in the right gap and a resistance coil dipped in water (in a beaker) in the left gap, the balancing length obtained is '1'. If the temperature of water is increased, the new balancing
View SolutionIn an experiment on the measurement of internal resistance of as cell by using a potentionmeter, when the key K is kept open then balancing length is obtained at y metre. When the key K is closed and some resistance R is inserted in the resistance box, then the balancing length is found to be x metre. Then the internal resistance is
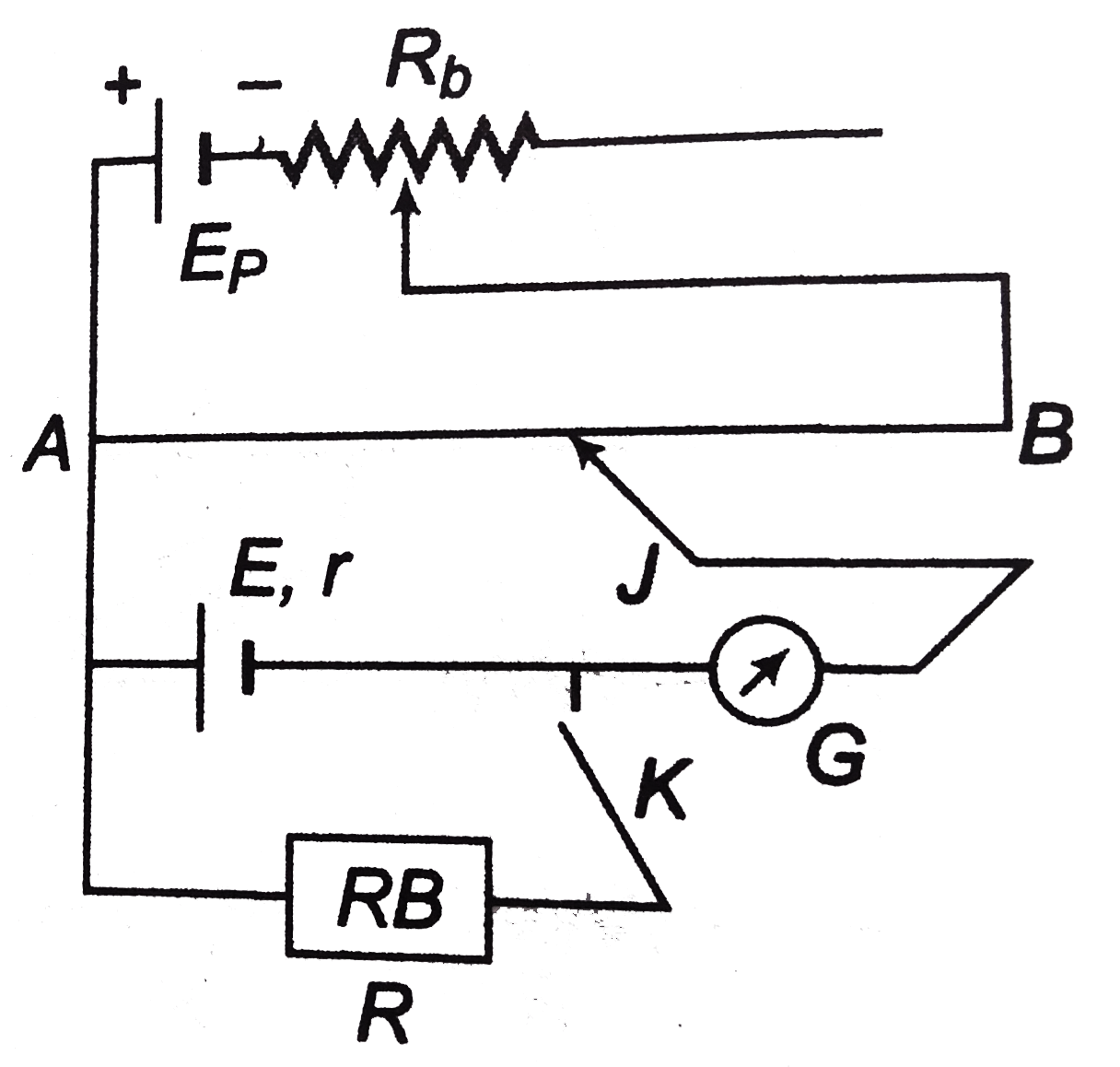 View Solution
View Solution

