In the given network, the capacitor is initially undercharged and switch is kept open.

The switch is closed at t = 0. Write the expression of charge on the capacitor as a function of time.
q=CV(1−e−t/2RC)
q=2CV(1−e−t/2RC)
q=CV(1−e−t/2RC)
q=CV(1−e−2t/3RC)
The correct Answer is:A
The branch of circuit containing resistance alone is connected in parallel to the branch containing capacitor and the ideal battery is connected across both the branches. We can assume the branch containing the capacitor is independently connected to battery of emf E and thus the time constant for charging the cpacitor becomes τ=2RC. Steady state charge on the capacitor is CV, and this comes on it after a long time when there is no current through the branch containing capacitor. Using standard expression q=q0(1−e−t/τ), we can write q=CV(1−e−t/2RC).
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION FOR COMPETITIVE EXAMINATIONS)
20 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
45 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (NUMERICAL PROBLEMS)
24 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
In precious question the switch is kept closed for a long time and then assume it is opened at t = 0. Write the expression of charge on the capacitor as a function of time.
Aq=2CVe−t/3RCBq=CVe−t/3RCCq=CVe−t/2RCDq=CVe−2t/3RCThe switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
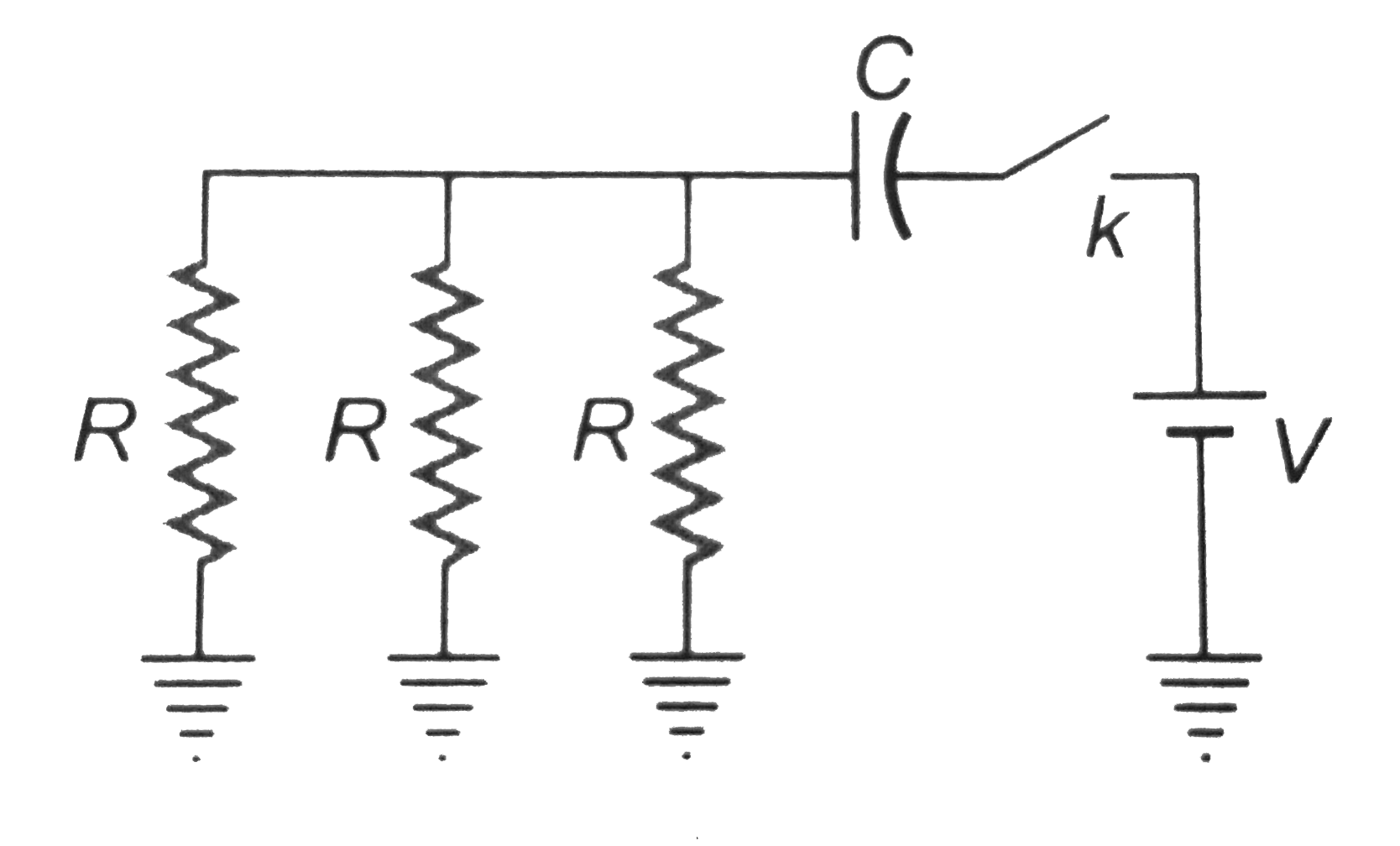 ACV(1−e−tRC)B3CV(1−e−tRC)CCV(1−e−3tRC)DCV(1−e−t3RC)
ACV(1−e−tRC)B3CV(1−e−tRC)CCV(1−e−3tRC)DCV(1−e−t3RC)At t<0, the capacitor is charged and the switch is opened.At t=0 the switch is closed.The shortest time T at which the charge on the capacitor will be zero is given by:
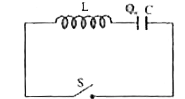 Aπ√LCB32π√LCCπ2√LCD2π√LC
Aπ√LCB32π√LCCπ2√LCD2π√LC
Consider the situation shown in figure.The switch is closed at t=0when the capacitor C1as a function of time t.
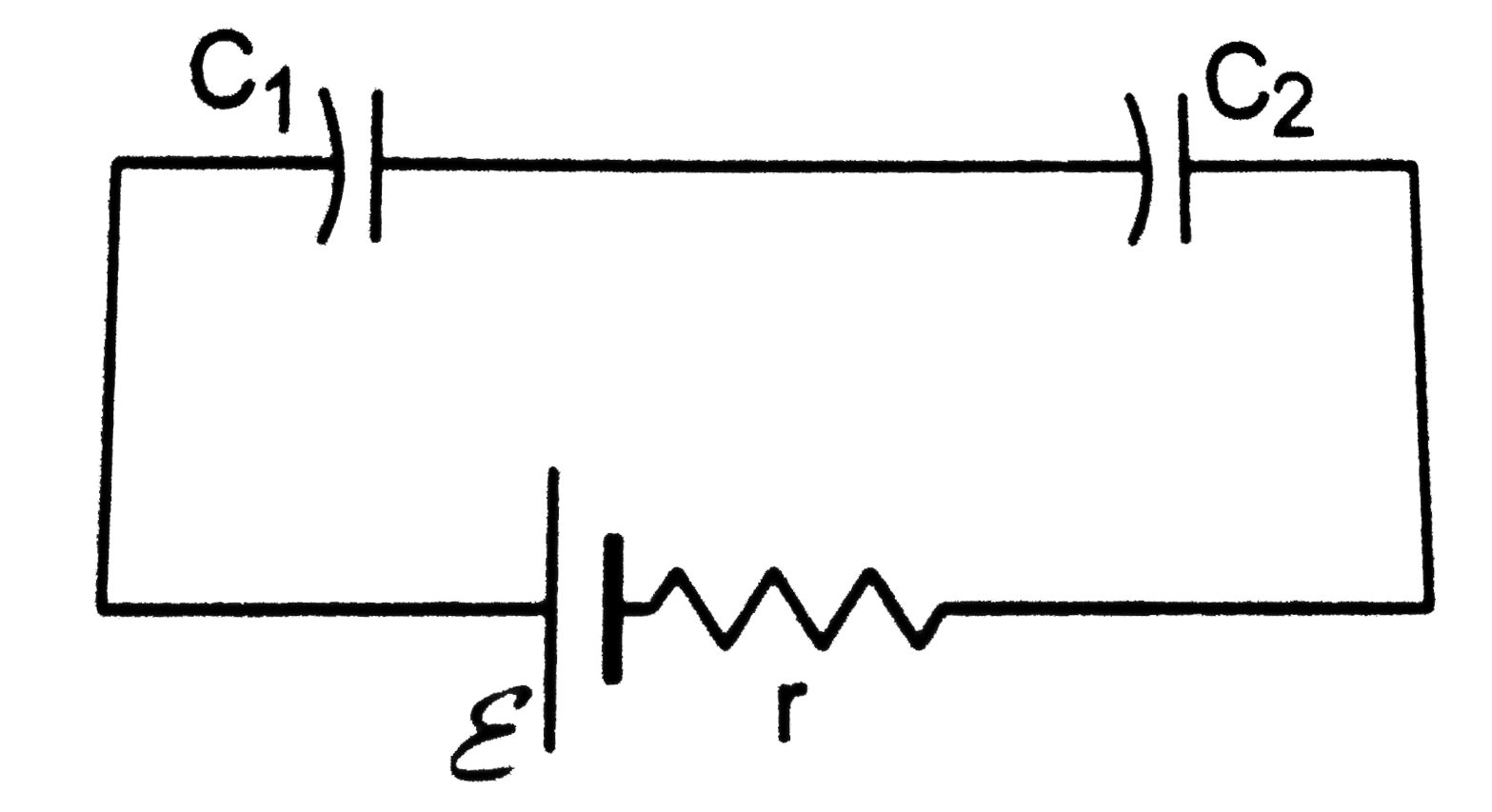
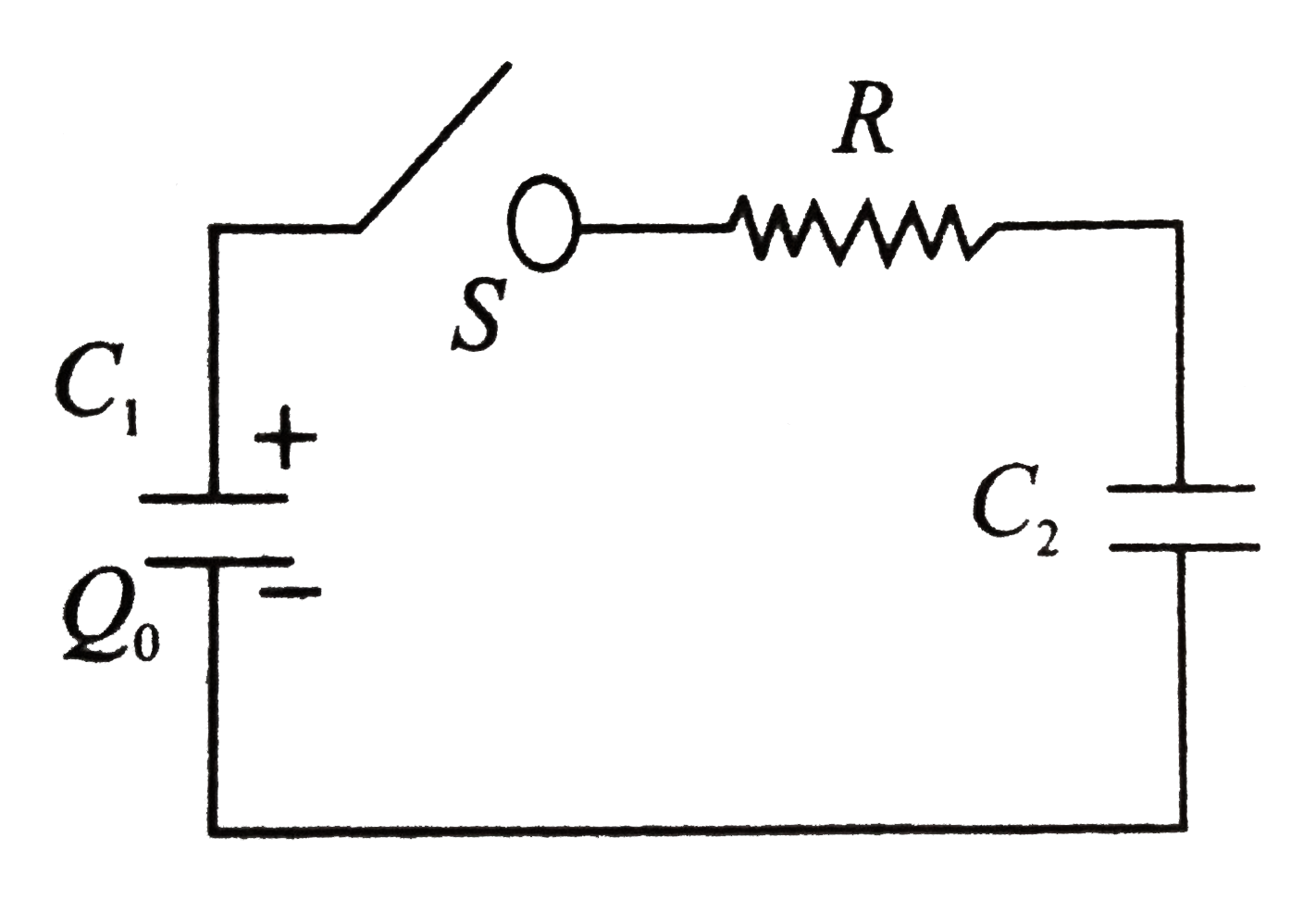
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
View SolutionIn the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is

View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is

View SolutionIn the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is

View Solution

