Here is a circuit for transient analysis of current flowing in several branches.

Given that the switch Sw is turned on at t = 0, make appropriate calculations to answer the following questions.
Current flowing in the branch containing capacitor as a finction of time.
V3Re−2t3RC
V2Re−2t3RC
2V3Re−3t2RC
V3Re−t3RC
The correct Answer is:A

The flow of current is shown in the figure for a transient state of capacitor when charging of the capacitor is not yet complete. We have assumed q as the instantaneous charge on the capacitor. Applying Krichhoff.s for loop ABCDEFA we get the following equation:
V=i1R−qC−iR=0...(i)
Now applying Krichhoff.s law for loop ABCFA we get the following equation:
V−(i−i1)R−iR=0⇒V−2iR+i1R=0
⇒2iR=V+i1R⇒i=V+i1R2R
⇒i=V2R+i12 ...(ii)
Substitution .i. from equation (ii) in equation (i) we get the following:
V−i1R−qC−(V2R+i12)R=0
⇒V−i1R−qC−V2−i1R2=0
⇒V2−qC=i1R+i1R2⇒V2−qC=3i1R2
⇒CV−2q=3i1RC ...(iii)
Further we can write the current flowing in branch containing capacitor as the rate of storage of charge in capacitor.
i1=dqdt ...(iv)
Substituting from equation (iv) in equation (iii) we get the following:
CV−2q=3RCdqdt
⇒dqCV−2q=dt3RC
⇒a∫0dqCV−2q=t∫0dt3RC
⇒[−12ln(CV−2q)]q0=t3RC
⇒ln(CV−2q)CV=−2t3RC
⇒CV−2qCV=e−2t3RC
⇒q=CV2(1−e−2t3RC)
⇒q=CV2(1−e−2t3RC)...(v)
Thus, charge stored by the capacitor as a function of time is given by:
q=CV2(1−e−2t3RC)
From this equation it is clear that the time constant for given circuit is given by:
τ=3RC/2
On differentiationg the charge we can calculate current flowing in the branch of capacitor which is represented as i1 in this case.
⇒i1=dqdt=CV2(0−23RCe−2t3RC)
⇒i1=V3Re−2t3RC ...(vi)
Now substituting value of i1 from equation (vi) in equation (ii) we get the following:
⇒i=V2R+i12=V2R+V6Re−2t3RC
⇒i=V6R(3+e−2t3RC) ...(vii)
Thus, the current supplied by the battery is given by,
i=V6R(3+e−2t3RC)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS ASSERTION REASON TYPE QUESTIONS)
10 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS MATRIX MATCH TYPE QUESTIONS)
1 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (C. MULTIPLE CHOICE QUESTIONS WITH MORE THAN ONE CORRECT ANSWER)
18 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A capacitor of capacitance C is connected to a battery of emf V through a resistance R with a switch connected in series .Switch is turned on at t=0 . Find the displacement current flowing between the plates of capacitor as a function of time .
View SolutionAt t=0 , switch S is closed. Find time constant of the circuit and current through inductor as a function of time t .

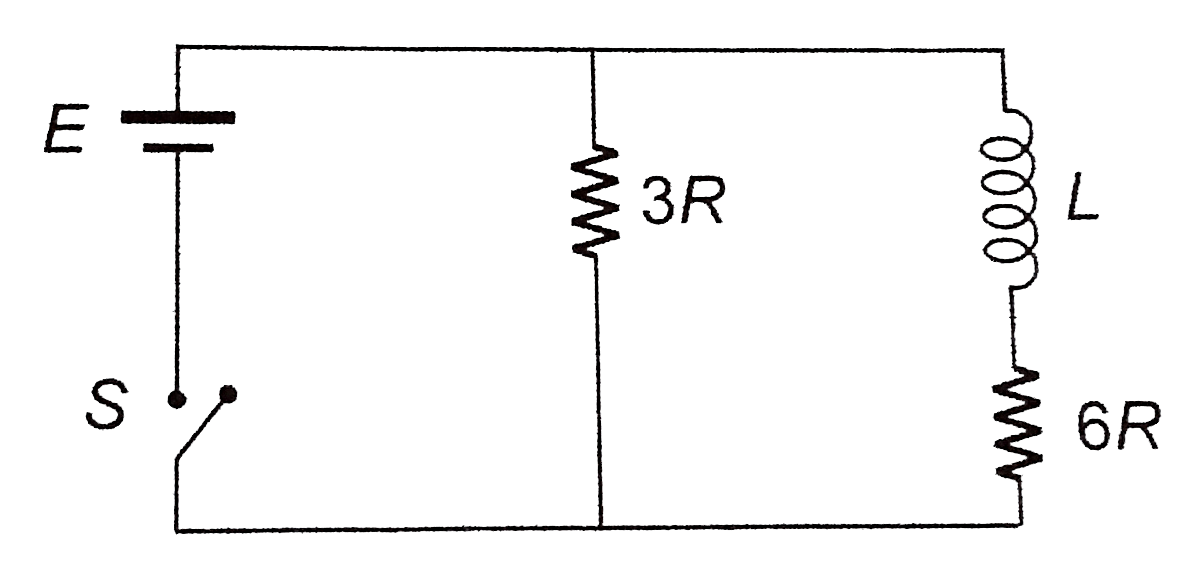
View Solution
Knowledge Check
A part of a circuit in steady state along with the currents flowing in the branches,the values of resistances,etc, is shown in figure.Calculate the energy stored in the capacitor.
 A8×10−1JB8×10−2JC8×10−3JD8×10−4J
A8×10−1JB8×10−2JC8×10−3JD8×10−4J
A part of a circuit in steady state along with the currents flowing in the branches,the values of resistances,etc, is shown in figure.Calculate the energy stored in the capacitor.

View Solution
A part of the circuit in a steady state along with the currents flowing in the branches, the values of resistance, etc. is shown in the figure. Calculate the energy stored in the capacitor.
View SolutionThe switch S of the circuit is closed at t = 0. Find the current (in Amp.) through the capacitor when the switch S is closed at t = 0

View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionA part of a circuit in steady state along with the currents flowing in the branches,the values of resistances,etc, is shown in figure.Calculate the energy stored in the capacitor.

View SolutionA part of a circuit in steady state along with the currents flowing in the branches,the values of resistances,etc, is shown in figure.Calculate the energy stored in the capacitor.

View Solution
