A capacitor of capacitance C1=3C is charged to a potential difference V and connected to an unchanged capacitor of capacitance C2=C through a resistor of resistance R and a switch. Switch is turned on at t = 0.

Calculate the rate of heat generation across the resistor R
V2Re−8t3RC
V2Re−4t3RC
V22Re−8t3RC
V22Re−4t3RC
The correct Answer is:A
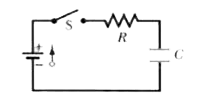
Here is the circuit diagram showing current and charges on the capacitor in a transient state.

Let q be the instantaneous charge on capacitor C2, then according to charge conservation 3CV−q must be the remaining charge on capacitor C1 because initial charge with the capacitor C1 is 3 CV.
Applying Krichhoff.s law for the loop ADCBA
−qC−iR+3CV−q3C=0
⇒−qC−R+V−q3C=0
⇒V−4q3C=0R
⇒3CV−4q=i(3RC)..(i)
We can write i=dq/dt in equation (1) to get the following
3CV−4q=dqdt3RC⇒dq3CV−4q=dt3RC
⇒q∫0dq3CV−4q=t∫0dt3RC
⇒[−14ln(3CV−4q)]q0=t3RC
⇒ln((3CV−4q))3CV=−4t3RC
⇒(3CV−4q)3CV=e4t3RC
⇒q=3CV4(1−e4t3RC) ...(ii)
Current flowing in the circuit can be calculated by differentiating charge:
⇒i=dqdt=3CV4(0+43RCe4t3RC)
⇒i=VRe4t3RC...(iii)
The rate of heat generation across resistance as a function of time can be written as follows:
H=i2R
⇒H=V2Re8t3RC...(iv)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS ASSERTION REASON TYPE QUESTIONS)
10 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS MATRIX MATCH TYPE QUESTIONS)
1 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (C. MULTIPLE CHOICE QUESTIONS WITH MORE THAN ONE CORRECT ANSWER)
18 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
View SolutionA capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
View Solution
Knowledge Check
A capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is VRBThe current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)CThe charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)DAfter a long time, the potential difference across the capacitor C1is(C1C1+C2)VA capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
A12C0V20B13C0V20C16C0V20D18C0V20A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
Switch S in Fig. 27-46 is closed at time t= 0, to begin charging an initially uncharged capacitor of capacitance C=49.0μF through a resistor of resistance R=32.0Ω. At what time is the potential across the capacitor equal to that across the resistor?
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View SolutionA charged capacitor of capacitance C is discharging through a resistor of resistance R. At what time the charge on the capacitor is equal to one half of its initial value?
View SolutionA capacitor of capacitance C0 is charged to a potential V0 and is connected with another capacitor of capacitance C as Shown . After closing the switch S, the common potential across the two capacitors becomes V . The capacitance C is given by

View Solution
