Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage 'DelataV' development between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E =ρJ, where J is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.

Now answer the following questions based on the above passage.
ΔV measured between B and C is:
ρI2π(a−b)
ρIπa−ρIπ(a+b)
ρIa−ρI(a+b)
ρI2πa−ρI2π(a+b)
The correct Answer is:B

Current entering at a point on a conducting slab is spread in a hemispheriacal region. Let electric field intensity at a distance r from the current entry point is E then from microscopic version of Ohm.s law we can write:
E=ρJ=ρ(I/2πr2)=ρI2πr2
So electric field intensity at a point distance r from the current entry point is E=ρI2πr2 in radial outward direction. This is the answer for Q2 of the passage. Option (d) is correct. To calculate the potential difference for question 1 of the passage we need to use the above result of electric field. Direction of electric field along the line AD will be direction from A towards D in the direction of current. The same direction of electric field will be there due to current I leaving the point D of the slab.
We need to write electric field at a point distance r from point A then the same point will be at a distance (2a+b−r) from the point D.
Net electric field
E=ρI2πr2+ρI2π(2a+b−r)2
Let dV be the potential difference obtained if we move further a distance dr towards D from A at a distance r from A. We can write the following equation:
dV=−→E.d→r=−ρI2π[1r2+1(2a+b−r)2]dr
We can integrate the above relation from r = a to r=a+b to find the potential difference between B and C.
VC∫VBdV=−ρI2πa+b∫a[1r2+1(2a+b−r)2]dr
⇒VC−VB=−ρI2πa+b∫a[1r2+1(2a+b−r)2]dr
⇒VB−VC=ρI2πa+b∫a[1r2+1(2a+b−r)2]dr
⇒VB−VC=ρI2π[−1r+−1(−1)(2a+b−r)]a+ba
⇒VB−VC=ρI2π[1(2a+b−r)−1r]a+ba
⇒VB−VC=ρI2π[{1(2a+b−a−b)−1a+b}−{1(2a+b−a)−1a}]
⇒VB−VC=ρI2π[{1a−1a+b}−{1(a+b)−1a}]
⇒VB−VC=ρIπ[{1a−1a+b}]=ρIπa−ρIπ(a+b)
Option (b) is correct for question D12. Note that we can also write the above result as follows
VB−VC=ρIbπa(a+b)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS ASSERTION REASON TYPE QUESTIONS)
10 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS MATRIX MATCH TYPE QUESTIONS)
1 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (C. MULTIPLE CHOICE QUESTIONS WITH MORE THAN ONE CORRECT ANSWER)
18 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
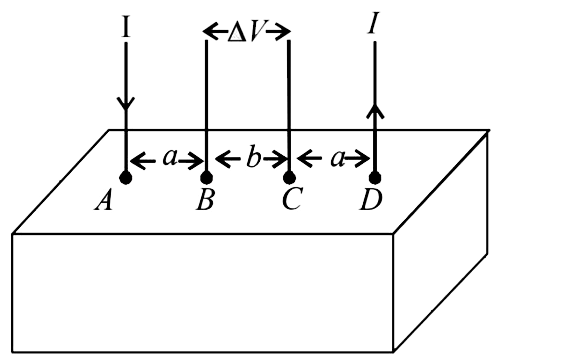
Delta V measured between B and C is
View SolutionPassage-II:
Consider a block conducting material of resistivity .ρ. shown in the figure. Current .I. enters at .A. and leaves from .D.. We apply superposition principle to find voltage .ΔV. developed between .B. and .C.. The calculation is done in the following steps :
i) Take current .I. entering from .A. and assume it to spread over a hemispherical surface in the block.
ii) Calculate field E(r ) at distance .r. from A by using Ohm.s law E=ρj, where j is the current per unit area at .r..
iii) From the .r. dependence of E(r ), obtain the potential V(r ) at r.
iv) Repeat (i), (ii), (iii) for current .I. leaving .D. and superpose results for .A. and .D..
For current entering at A the electric field at a distance .r. from A is
View Solution
Knowledge Check
Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.

Delta V measured between B and C isAρIπa−ρIπ(a+b)BρIa−ρIa+bCρI2πa−ρI2π(a+b)DρI2π(a−b)Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
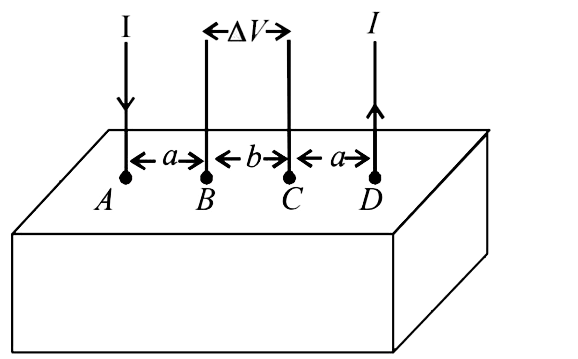
For current entering at A, the electric field at a distance 'r'AρI8πr2BρIr2CρI2πr2DρI4πr2When some potential differece is maintained between A and B, current I enters the network at A and leaves at B
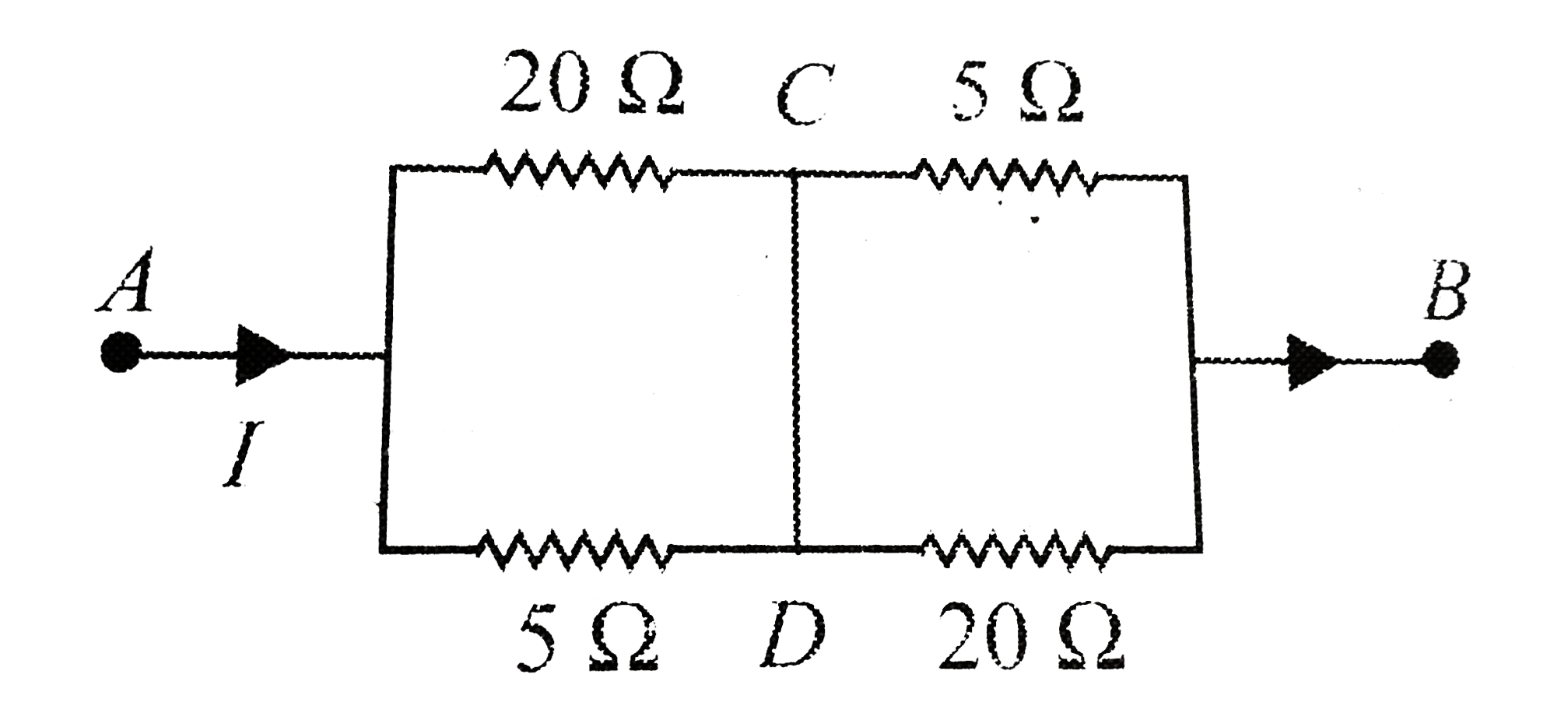 AThe equivalent resistance between A and B is 8Ω.BC and D are at the same potential.CNo current flows between C and D.DCurrent 3I/5 flows from D to C.
AThe equivalent resistance between A and B is 8Ω.BC and D are at the same potential.CNo current flows between C and D.DCurrent 3I/5 flows from D to C.
From the following calculate (i) Current ratio , and (ii) Quick ratio:

View SolutionWhen some potential differece is maintained between A and B, current I enters the network at A and leaves at B
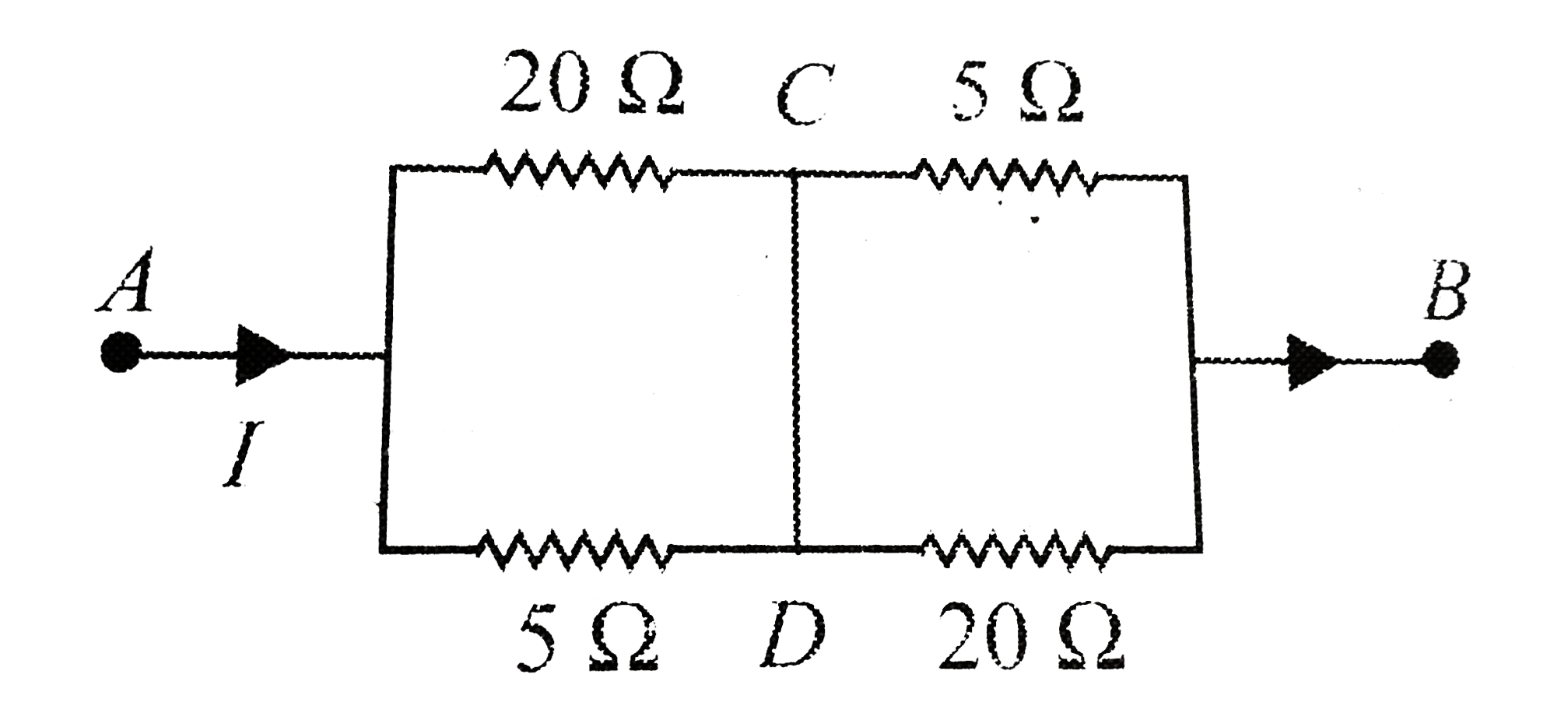
View Solution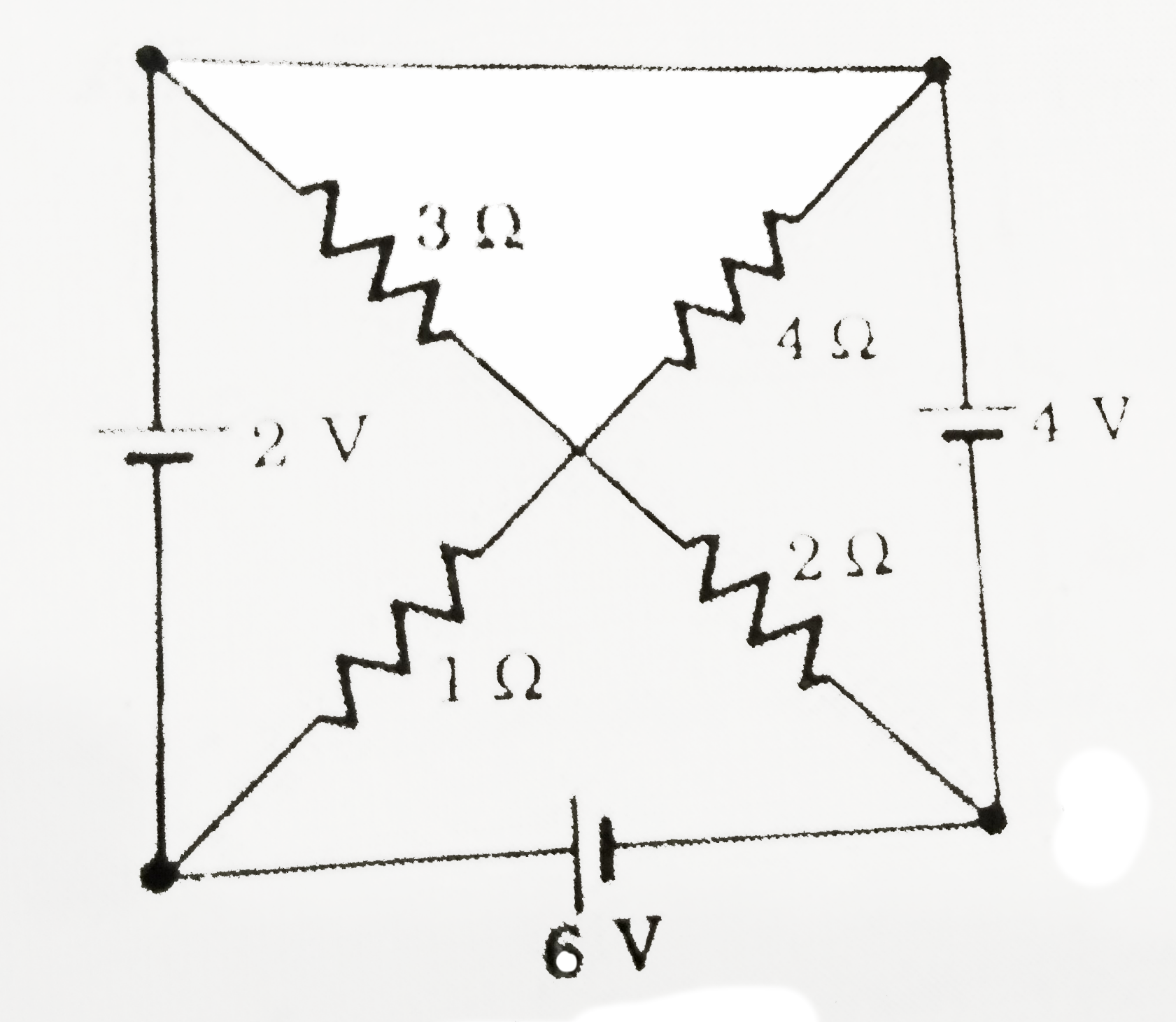
In the network shown in figure. (i) calculate the current of the 6V battery and (ii) determine the potential difference between the points A and B.
View SolutionA current carrying wire is placed in the grooves of an insulating semicircular disc of radius 'R', as shown in Fig. The current enters at point A and leaves from point B. Determine the magnetic field at Point D.
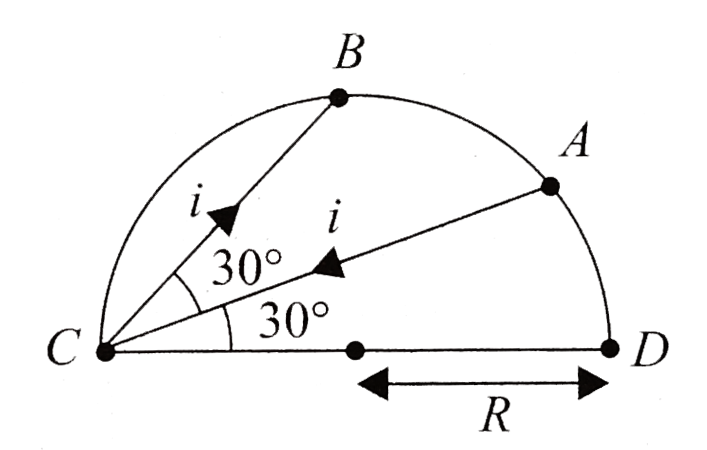
View SolutionA current carrying wire is placed in the grooves of an insulating semicircular disc of radius 'R', as shown in Fig. The current enters at point A and leaves from point B. Determine the magnetic field at Point D.

View Solution
