The length of tangent from a point A at a distance of 12 cm from the centre of the circle is 9 cm. What is the radius of the circle ?
The correct Answer is:3√7
To find the radius of the circle, we can use the Pythagorean theorem. Let's denote:
- O as the center of the circle
- A as the point outside the circle from which the tangent is drawn
- B as the point where the tangent touches the circle
We know the following:
- The distance OA (from the center O to point A) = 12 cm
- The length of the tangent AB = 9 cm
- The radius OB = r (which we need to find)
Since the radius OB is perpendicular to the tangent AB at point B, triangle OAB is a right triangle. According to the Pythagorean theorem:
OA2=OB2+AB2
Substituting the known values:
1. OA=12cm
2. AB=9cm
Now, substituting these values into the equation:
122=OB2+92
Calculating the squares:
144=OB2+81
Now, isolate OB2:
OB2=144−81
Calculating the right side:
OB2=63
Taking the square root of both sides to find OB:
OB=√63
We can simplify √63:
OB=√9×7=3√7cm
Thus, the radius of the circle is:
Radius=3√7cm
- A as the point outside the circle from which the tangent is drawn
- B as the point where the tangent touches the circle
- The length of the tangent AB = 9 cm
- The radius OB = r (which we need to find)
2. AB=9cm
Topper's Solved these Questions
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Short Answer Questions - II 3 mark)
22 Videos
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Long Answer Questions 4 mark)
12 Videos
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Very Short Answer Questions 1 mark)
13 Videos
- ARITHMETIC PROGRESSIONS BOOK - VK GLOBAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - SELF ASSESSMENT TEST
10 Videos
- COORDINATE GEOMETRY BOOK - VK GLOBAL PUBLICATIONCHAPTER - COORDINATE GEOMETRY EXERCISE - SELF-ASSESSMENT TEST
10 Videos
Similar Questions
Knowledge Check
A chord of length 60 cm is at a distance of 16 cm from the centre of a circle . What is the radius (in cm ) of the circle ?
A17B34C51D68A chord of length 120 cm is at a distance of 32 cm from the centre of a circle. What is the radius (in cm) of the circle?
A96B34C72D68A chord of length 120 cm is at a distance of 32 cm from the centre of a circle. What is the radius (in cm) of the circle?
A96B34C72D68
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
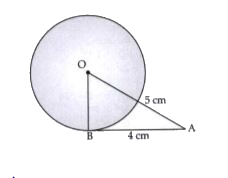
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View SolutionFind the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
View SolutionIn a circle of radius 13 cm , a chord is at a distance of 12 cm from the centre of the circle. What is the length of the chord?
13 सेमी त्रिज्या वाले एक वृत्त में, वृत्त के केंद्र से 12 सेमी की दूरी पर एक जीवा है | जीवा की लंबाई ज्ञात करें |
View SolutionThe length of a tangent drawn from a point 10 cm away from the centre of the circle of radius 5 cm is
View Solution

