In the given figure, is shown a sector OAP of a circle with centre 0, containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r[tanθ+secθ+πθ180−1]
Step by step video & image solution for In the given figure, is shown a sector OAP of a circle with centre 0, containing /_ theta. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r[tan theta + sec theta + pi theta/180 - 1] by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - HOTS (Higher Order Thinking Skills)
6 Videos
- AREAS RELATED TO CIRCLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Proficiency Exercise (Very Short Answer Questions)
10 Videos
- AREAS RELATED TO CIRCLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Short Answer Questions -II
30 Videos
- ARITHMETIC PROGRESSIONS BOOK - VK GLOBAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - SELF ASSESSMENT TEST
10 Videos
Similar Questions
In Fig. 4, a sector OAP of a circle with centre O, containing ∠0. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r.
[tan 0 + sec 0 + π0180∘−1]
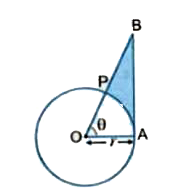
View SolutionFigure shows a sector of a circle, centre O, containing an angle θ. Prove that (i) Perimeter of the shaded region is r(tanθ+secθ+πθ180−1) (ii) Area of shaded region is r22(tanθ−πθ180)
View SolutionFigure shows a sector of a circle of radius r containing an angle θ∘ The area of the sector is Acm2 and the perimeter is 50cm. Prove that θ=360π(25r−1) and A=25r−r2
View SolutionFig. 15.17, shows a sector of a circle, centre O , containing an angle θo , prove that: (FIGURE) (i) Perimeter of the shaded region is r (tanθ+secθ+πθ180−1) (ii) Area of the shaded region is r22 (tanθ−πθ180)
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionEliminate θ from the equations asecθ+btanθ+c=0 and psecθ+qtanθ+r=0
View SolutionEliminate θ between the equation a secθ+btanθ+c=0 and psecθ+qtanθ+r=0
View SolutionProve that-
sec2θ−1−tan2θ=0
View SolutionIn the diagram as shown, a circle is drawn with centre C(1, 1) and radius I and a line L. The line Lis tangential to the circle at Q. Further L meet the y-axis at R and the x-axis at Pis such a way that the angle OPQ equals θ where 0<θ<π2 The coordinates of Q are
View SolutionIn the given figure ,If ∠ACB=θandtanθ=12 then the relation between x , a , and b is
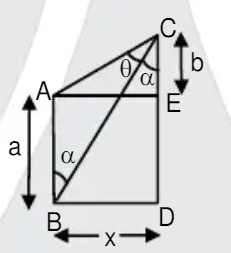
View Solution
