Question

The length of tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What will be the radius of the circle ?

Answer

3 cm

Explanation

To find the radius of the circle given the length of the tangent and the distance from the center, we can use the Pythagorean theorem. Here’s a step-by-step solution:

Step 1: Understand the problem
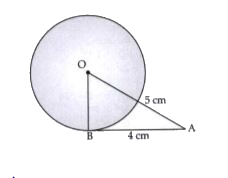
We have a point A outside the circle, which is 5 cm away from the center O of the circle. The length of the tangent AT from point A to the circle is 4 cm.

Step 2: Identify the right triangle
When a tangent is drawn from a point outside the circle to the point of tangency, it forms a right triangle with the radius and the line segment from the center to the point outside the circle. In this case, triangle OAT is a right triangle where:
- OA = 5 cm (distance from the center to point A)
- AT = 4 cm (length of the tangent)
- OT = r (radius of the circle, which we need to find)

Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem:
\( OA^2 = OT^2 + AT^2 \)
Substituting the known values:
\( 5^2 = r^2 + 4^2 \)

Step 4: Calculate the squares
Calculating the squares:
\( 25 = r^2 + 16 \)

Step 5: Solve for r²
Now, we can rearrange the equation to find r²:
\( r^2 = 25 - 16 \)
\( r^2 = 9 \)

Step 6: Find the radius
Taking the square root of both sides gives us:
\( r = \sqrt{9} = 3 \text{ cm} \)

Final Answer
The radius of the circle is 3 cm.

---