Question

Consider Example 6.8 taking the coefficient of friction, u, to be ${\displaystyle 0.5}$ and calculate the maximum compression of the spring.

Explanation

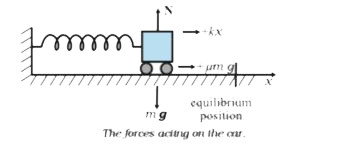
In presence of friction, both the spring force and the frictional force act so as to oppose the compression of the spring as shown in Fig. 6.9.
We invoke the work-energy theorem, rather than the conservation of mechanical energy.
The change in kinetic energy is
`triangleK= K_(f)-K_(t)= 0-(1)/(2)mv^(2)`
The work done by the net force is
`W= -(1)/(2)kx_(m)^(2)- mu mg x_(m)`
Equatting we have
`(1)/(2)mv^(2)= (1)/(2)k x_(m)^(2)+ mu mg x_(m)`
Now `mu mg= 0.5xx10^(3)xx10= 5xx 10^(3)N` (taking `g= 10.0 ms^(-2)`). After rearranging the above equation we obtain the following quadratic equation in the unknown `x_(m)`.
`kx_(m)^(2)+ 2 mu mg x_(m)- mv^(2)= O`
`x_(m)=(-mu mg+[mu^(2)m^(2)g^(2)+mkv^(2)]^(1/2))/(k)`
where we take the positive square root since `x_(m)` is positive. Putting in numerical values we obtain `x_(m)= 1.35m`
which, as expected, is less than the result in Example 6.8.
If the two forces on the body consist of a conservative force `F_(c )` and a non-conservative force `F_(nc)`, the conservation of mechanical energy formula will have to be modified. By the WE theorem
`(F_(c )+F_(nc)) trianglex= triangleK`
But `F_(c ) triangle x= -triangle V`
Hence, `triangle(K+V)= F_(nc) triangle x`
`triangle E= F_(nc) trianglex`
where E is the total mechanical energy. Over the path this assumes the form
`E_(f)-E_(t)= W_(nc)`
where `W_(nc)` is the total work done by the non-conservative forces over the path. Note that unlike the conservative force, `W_(nc)` depends on the particular path i to f.