Given in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
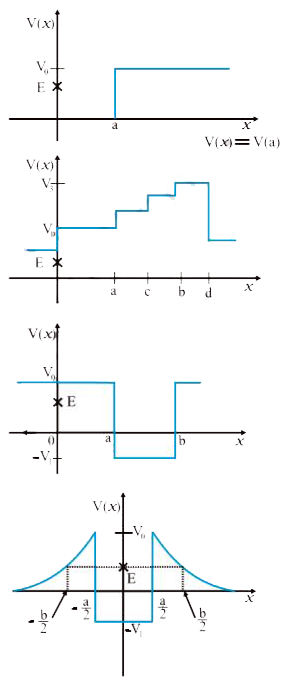
(a) x>a,0
(b) −∞<x<∞,V1
(c ) x<a,x>b,−V1
(d) −b/2<x<−a/2,a/2<x<b/2,−V1.
Similar Questions
Given in fig are examples of some potential energy functions in one dimension. The total enrgy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
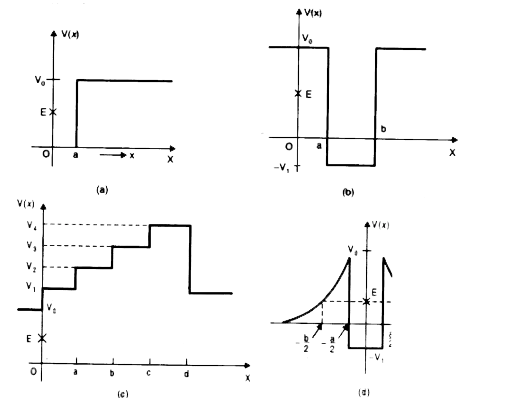
View SolutionGiven in fig are examples of some potential energy functions in one dimension. The total enrgy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
View Solution
Knowledge Check
- Question 1 - Select One
A particle with total energy E moves in one dimemsional region where the potential energy is U(x) The speed of the particle is zero where
AU(x)=0BU(x)=ECdU(x)dx=0Dd2U(x)dx2=0 - Question 2 - Select One
The total energy of a particle having a displacement x, executing simple harmonic motion is
A∝xB∝x2Cindependent of xD∝x1/2 - Question 3 - Select One
A particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
AU(x)>EBE(x)<ECU(x)=0DU(x)≤E
The total energy of a particle having a displacement x, executing simple harmonic motion is
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View SolutionWhen displacement of a particle executing SHM is half of the amplitude,its potential energy is 5 J. Find the total energy of the particle in SHM,if potential energy at mean position is zero.
View SolutionA particle with total energy E moves in one direction in a region where, the potential energy is U The acceleration of the particle is zero, where,
View SolutionThe potential energy of a particle executing SHM in its rest position is 15 J. The average kinetic energy of the particle during one oscillation is 5 J. The total energy of the particle is
View Solution