Two vessels have the same area but different shapes. The first shapes takes twice the volume of water that the second vessel requires to fill up to a particular common height? Is the force exerted by the water on the base of the vessel the same in the two cases? If so, why do the vessels filled with water to that same height give different readings on a weighing scale?
Pressure (and therefore force) on the two equal base areas are identical . But force is exerted by water on the sides of the vessels also. Which has a nonzero vertical component when the sides of the vessel are not perfectly normal to the base. Thus net vertical component of force by water on sides of the vessel is greater for the first vessel than the second. hence the vessels weigh different even when the force on the base is the same in the two cases.
Similar Questions
Two vessels have the same base area but differnent shapes. The first vessel takes twice the vloume of water that the second vessel requires to fill up to a paricular common height . Is the force exerted by water on the base of the vessel the same in the two case? If so, why do the vessels filled with water to that same height give different reading on a weighting scale ?
View SolutionTwo vessels have the same base area but differnent shapes. The first vessel takes twice the vloume of water that the second vessel requires to fill up to a paricular common height . Is the force exerted by water on the base of the vessel the same in the two case? If so, why do the vessels filled with water to that same height give different reading on a weighting scale ?
View Solution
Knowledge Check
Two vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
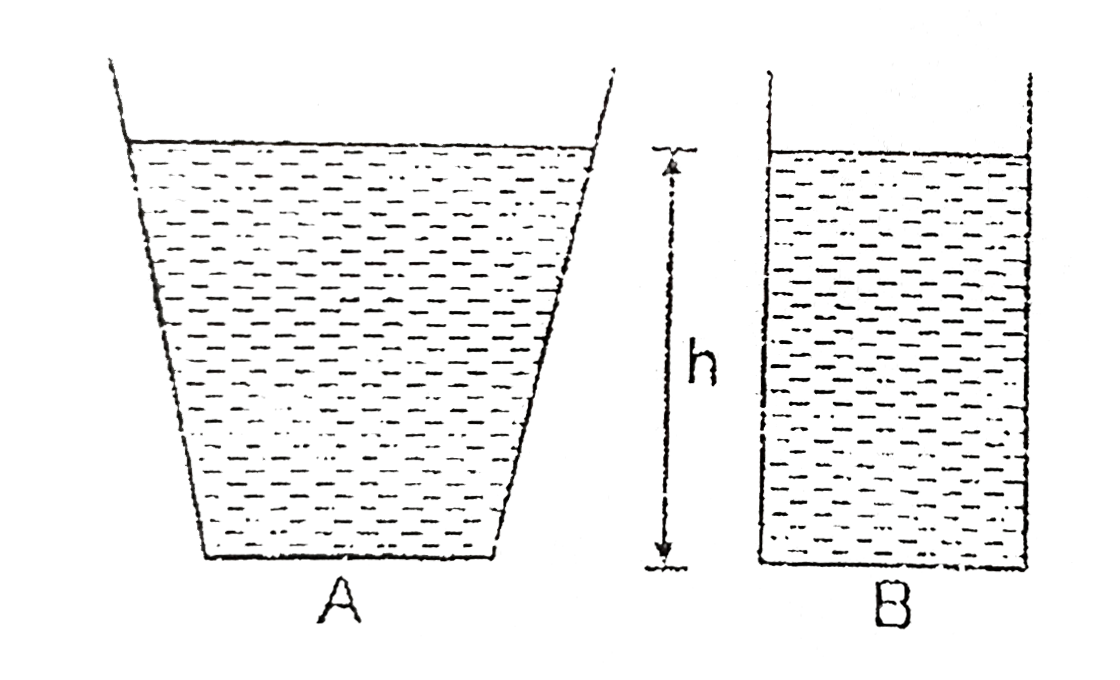 AFA>FB,WA>WBBFA=FB,WA>WBCFA=FB,WA<WBDFA>FB,WA=WB
AFA>FB,WA>WBBFA=FB,WA>WBCFA=FB,WA<WBDFA>FB,WA=WBTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
 AFA>FB,WA>WBBFA=FB,WA>WBCFA≡FB,WA<WBDFA>FB,WA=WB
AFA>FB,WA>WBBFA=FB,WA>WBCFA≡FB,WA<WBDFA>FB,WA=WBThree vessels A, B and C of different shapes contain water upto the same height in the figure. PA,PBandPC be the pressure exerted by the water at the bottom of the vessels A, B and C respectively. Then
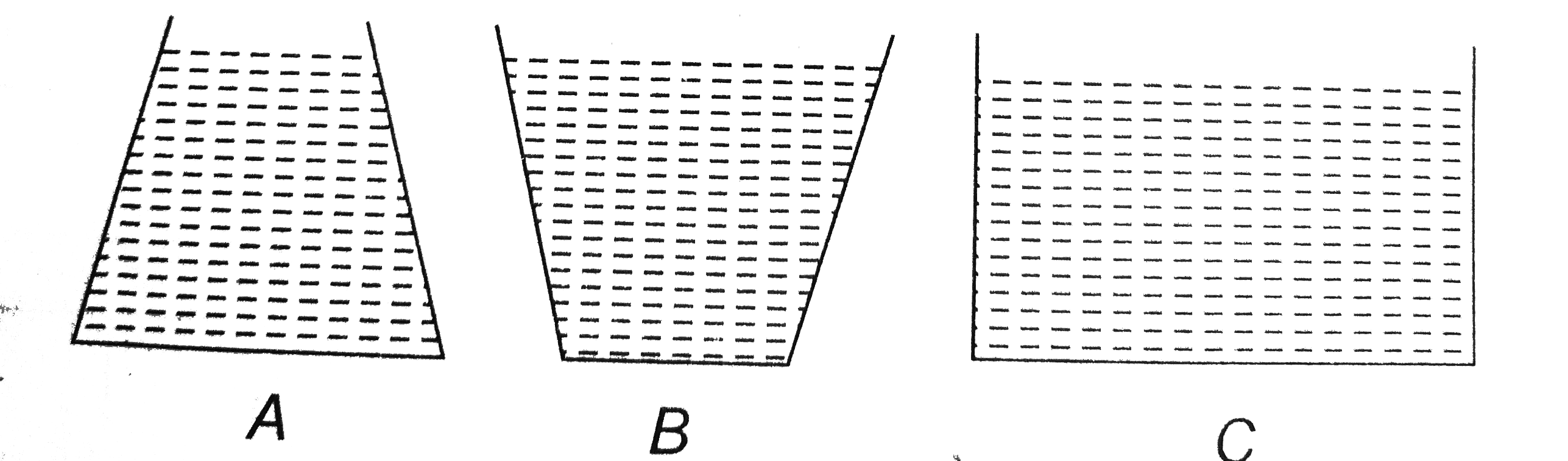 APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
Two identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same ?
View SolutionTwo identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same .
View SolutionTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then

View Solutionthe base of cylindrical vessel is hemesphericl in shape with rdius R . If the vessel is filled with liquid of density p up to a height h. calculate the thrust on the base.
View SolutionFour vessels A, B, C and D have different shapes and hold different amount of water. Which of the following is correct.

View Solution
