Two identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same ?
To determine whether the forces on the bases of the two vessels are the same, we can analyze the situation step by step.
1. Identify the Variables:
- Let the height of water in vessel 1 be h1 and in vessel 2 be h2.
- Both vessels have the same base area A.
2. Understand Pressure in Fluids:
- The pressure at the base of a column of liquid is given by the formula:
P=ρgh
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
3. Calculate Pressure at the Bases:
- For vessel 1, the pressure at the base P1 is:
P1=ρgh1
- For vessel 2, the pressure at the base P2 is:
P2=ρgh2
4. Calculate the Forces on the Bases:
- The force F1 on the base of vessel 1 is given by:
F1=P1×A=(ρgh1)×A
- The force F2 on the base of vessel 2 is given by:
F2=P2×A=(ρgh2)×A
5. Compare the Forces:
- Since the base areas A are the same, we can compare the heights:
F1=ρgh1A
F2=ρgh2A
- If h1>h2, then F1>F2.
6. Conclusion:
- Therefore, the forces on the bases of the two vessels are not the same. The statement that the forces on the bases of the two vessels are the same is false.
- Let the height of water in vessel 1 be h1 and in vessel 2 be h2.
- Both vessels have the same base area A.
- The pressure at the base of a column of liquid is given by the formula:
P=ρgh
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
- For vessel 1, the pressure at the base P1 is:
P1=ρgh1
- For vessel 2, the pressure at the base P2 is:
P2=ρgh2
- The force F1 on the base of vessel 1 is given by:
F1=P1×A=(ρgh1)×A
- The force F2 on the base of vessel 2 is given by:
F2=P2×A=(ρgh2)×A
- Since the base areas A are the same, we can compare the heights:
F1=ρgh1A
F2=ρgh2A
- If h1>h2, then F1>F2.
- Therefore, the forces on the bases of the two vessels are not the same. The statement that the forces on the bases of the two vessels are the same is false.
Similar Questions
Two identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid heigth is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
View SolutionEqual mass of three liquids are kept in three identical cylindrical vessels A, B and C. the densities are ρA,ρB,ρCwithρA<ρB<ρC. The force on the base will be
View SolutionTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
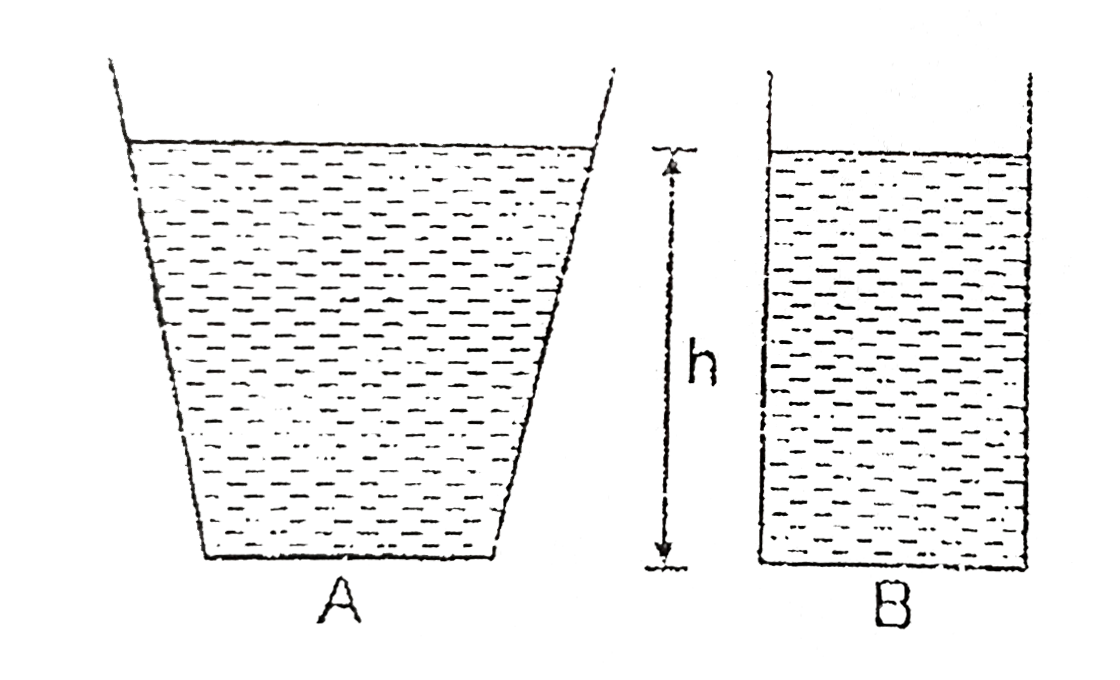
View SolutionTwo identical cylindrical vessel with their bases at the same level each contain a liquid of density ρ. The height of the liquid in one vessel is h1 and in the other is h2 the area of either base is A. What is the work done by gravity is equalising the levels when the two vessels are connected?
View SolutionTo what height h should a cylindrical vessel of diameter d be filled with a liquid so that the total force on the vertical surface of the vessel be equal to the force on the bottom-
View SolutionWater (p = 1000 kg/m3 ) and kerosene (a = 800kg/m3 ) are filled in two identical cylindrical vessels. Both vessels have small holes at their bottom. The speed of the water and kerosene coming out of their holes are v1 and v2 respectively. Select the correct alternative
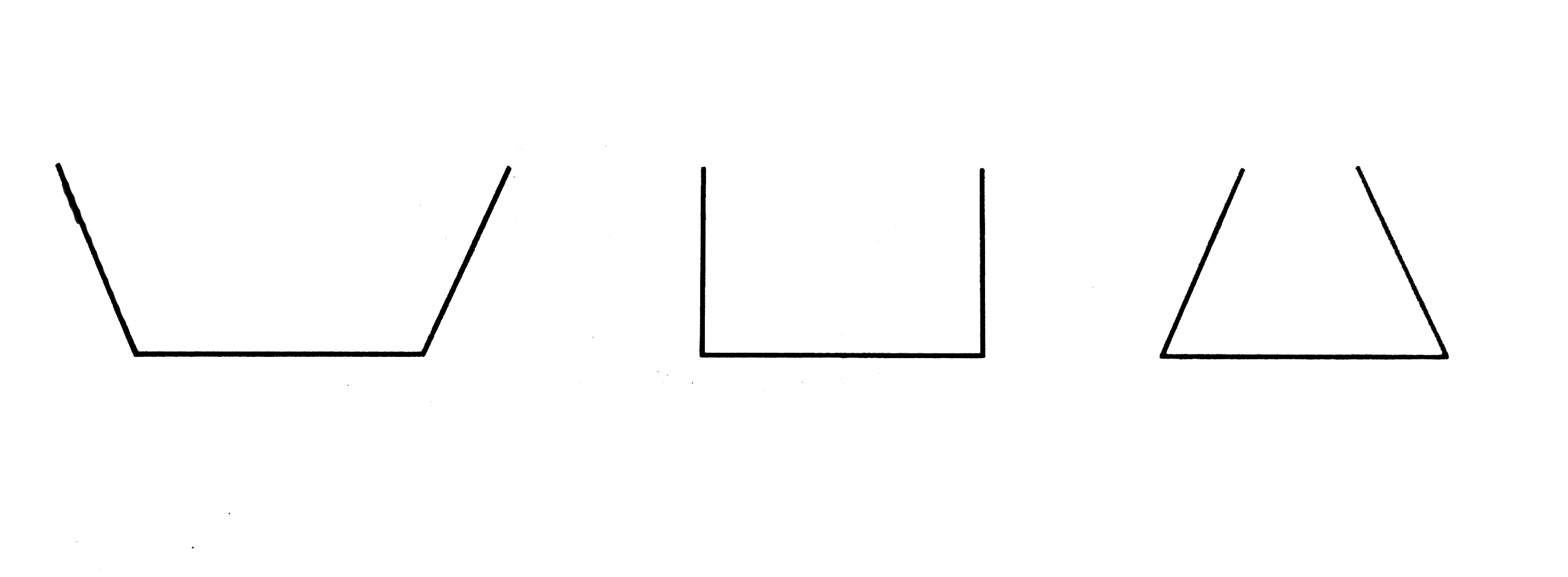
View SolutionThe three vessels shown in figure have same base area. Equal volumes of a liquid are poured in three vessels. The force on the base will be
View SolutionTwo identical vessels contain helium and hydrogen gases at same temperature, then
View SolutionA cylinder and a right circule cone are having the same bases and same height. The volume of the cylinder is the times the volume of the cone.
View SolutionA cone and a cylinder are having the same base. Find the ratio of their heights if their volumes are equal.
View Solution
