For a non-zero complex number z , let arg(z) denote the principal argument with π<arg(z)≤π Then, which of the following statement(s) is (are) FALSE? arg(−1,−i)=π4, where i=√−1 (b) The function f:R→(−π,π], defined by f(t)=arg(−1+it) for all t∈R , is continuous at all points of R , where i=√−1 (c) For any two non-zero complex numbers z1 and z2 , arg(z1z2)−arg(z1)+arg(z2) is an integer multiple of 2π (d) For any three given distinct complex numbers z1 , z2 and z3 , the locus of the point z satisfying the condition arg((z−z1)(z2−z3)(z−z3)(z2−z1))=π , lies on a straight line
arg(−1−i)=π4wherei=√−1
The function f: R ⇒(−π,π] defined by f(t) = arg (-1 it) for all t≠R is continuous at all points of R, where i=√−1
For any two non-zero complex numbers z1andz2arg(z1)+arg(z2) is an interger multiple of arg z1z2−arg(z1)+arg(z2) is an interger multiple of 2π
For any three given distinct complex number and z1,z2andz3 the locus of the point z satisfying the condition arg (z−z1)(z2−z3)(z−z3)(z2−z1)=π
The correct Answer is:A, B, D
Let z=-1-I and arg(z) = θ
Now tanθ=∣∣∣lim(z)Re(z)∣∣∣=∣∣∣−1−1∣∣∣=1
⇒θ=π4
Sincex<0,y>0
∴(z)=−(π−π4)=−3π4
(b) We have ,f(t) =arg (-1 + it )
arg(−1+it)=(π−tan−1t,t≥0),−(π+tan−1),t<0):}
This function is discontinuous at t = 0.
(c ) We have
arg(z1z2)−arg(z1)+arg(z2)+2nπ
∴arg(z1z2)−arg(z1)+arg(z2)
∴are(z1z2)−arg(z1)+arg(z2)
=arg(z1)−arg(z2)+2nπ−arg(z1)+arg(z2)
=2nπ
So given expression is multiple of 2π
(d) We have arg ((z−z1)(z2−z3)(z−z3)(z2−z1))=π
⇒(z−z1z−z3)(z2−z3z2−z1) is purely real
Thus , the points A(z1)B(z2),C(z3) and D(z) taken in order would be concylic if purely real .
Hence, it is a circle
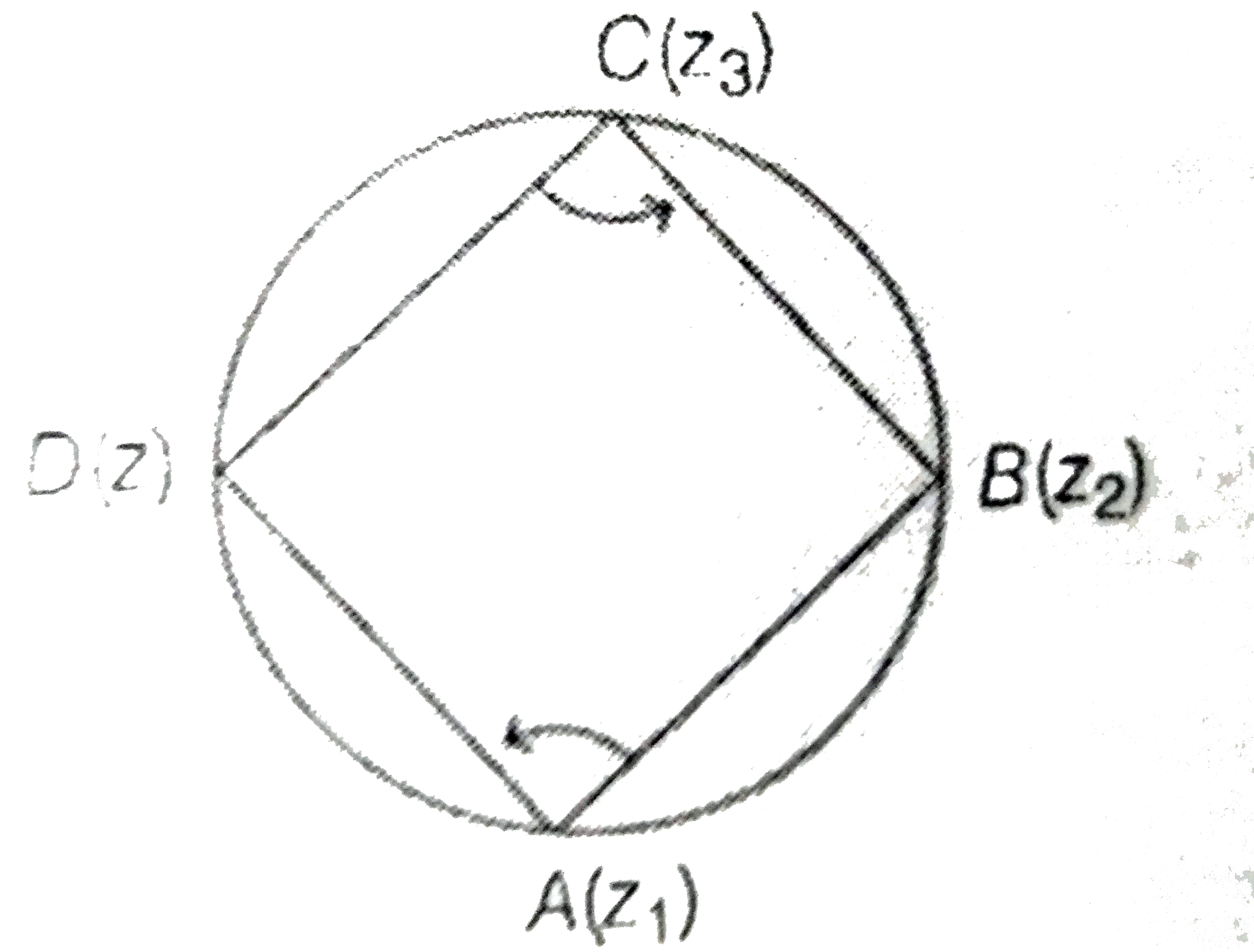
threrefore(a),(b),(d) are false statment.
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 3 ARGUMENT OF A COMPLEX NUMBER (OBJECTIVE QUESTIONS II)(MATCH THE COLUMNS )
1 Videos
- COMPLEX NUMBERSBOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 3 ARGUMENT OF A COMPLEX NUMBER (OBJECTIVE QUESTIONS II)()
1 Videos
- COMPLEX NUMBERSBOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 3 ARGUMENT OF A COMPLEX NUMBER (OBJECTIVE QUESTIONS I)(ONLY ONE CORRECT OPTION)
7 Videos
- CIRCLEBOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 5 Integer Answer type Question
1 Videos
- DEFINITE INTEGRATIONBOOK - IIT JEE PREVIOUS YEARCHAPTER - DEFINITE INTEGRATIONEXERCISE - LIMITS AS THE SUM
6 Videos
Similar Questions
Knowledge Check
If for complex numbers z1 and z2, arg z1−arg(z2)=0 then |z1−z2| is equal to
A|z1|+|z2|B|z1|−|z2|C||z1|−|z2∣D0If z1 and z2 are two non- zero comlex numbers such that |z1+z2|=|z1|+|z2| then arg (z1)−arg(z2) is equal to
A−πB−π2C0Dπ2If z1 and z2 are two non-zero complex numbers such that |z1+z2|=|z1|+|z2|, then arg(z1)-arg(z2) is equal to
A−π2B0C−πDπ2
If z1andz2, are two non-zero complex numbers such tha |z1+z2|=|z1|+|z2| then arg(z1)−arg(z2) is equal to
View SolutionLet z be a complex number such that the principal value of argument, argz>0. Then arg z-arg(-z) is
View SolutionIf z1 and z2 are two non-zero complex number such that |z1z2|=2 and arg(z1)−arg(z2)=π2 ,then the value of 3iz1z2
View SolutionFind the complex number z if arg(z+1)=π6 and arg(z−1)=2π3
View SolutionIf z ans w are two non-zero complex numbers such that |zw|=1 and arg (z) = arg (w) =π2,¯zw is equal to
View Solution
