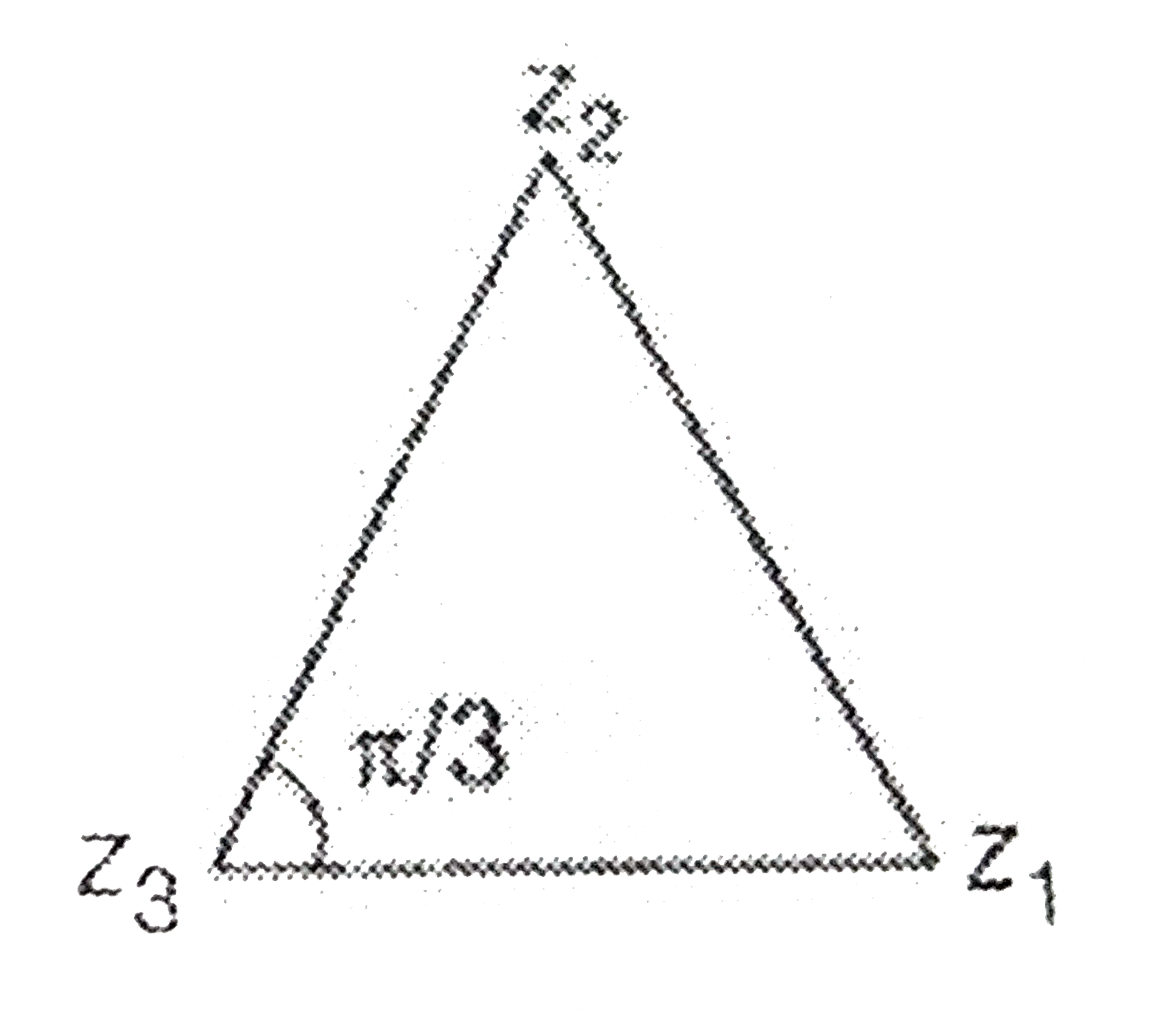
The complex numbers z1z2andz3 satisfying z1−z3z2−z3=1−i√32 are the vertices of triangle which is (1) of area zero (2) right angled isosceles(3) equilateral (4) obtuse angled isosceles
A
of area zero
B
right angled isosceles
C
equilateral
D
obtuse angled isosceles
Video Solution
Text Solution
The correct Answer is:C
z1−z3z2−z3=1−i√32=(1−i√3)(1+i√3)2(1+i√3)
=1−i232(1+i√3)
=42(1+i√3)
22(1+i√3)
⇒z2−z3z1−z3=1+√32=cosπ3+isinπ3
⇒∣∣∣z1−z3z1−z3∣∣∣=1andarg(z2−z2z1−z3)=π3
Hence the triangle is an equilateral .
Alternate solution
∴z1−z3z2−z3=1−i√32
⇒(z2−z1z1−z2)=π3andalso∣∣∣z2−z3z1−z3∣∣∣=1
Therefore , triangle is equilateral .
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 4 ROTATION OF A COMPLEX NUMBER (OBJECTIVE QUESTION II)(ONE OR MORE THAN ONE CORRECT OPTION)2videos
COMPLEX NUMBERS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 4 ROTATION OF A COMPLEX NUMBER (FILL IN THE BLANKS )3videos
COMPLEX NUMBERS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 3 ARGUMENT OF A COMPLEX NUMBER (OBJECTIVE QUESTIONS II)(ANALYTICAL & DESCRIPTIVE QUESTIONS )1videos
COMPLEX NUMBERS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 5 Integer Answer type Question1videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - DEFINITE INTEGRATIONEXERCISE - LIMITS AS THE SUM6videos
DEFINITE INTEGRATION
Similar Questions
Knowledge Check
- Question 1 - Select One
The complex number z1,z2andz3 satisfying z1−z3z2−z3=1−i√32 are the vertices of a triangle which is :
Aof area zeroBright - angled isoscelesCequilateralDobtuse - angled isosceles - Question 2 - Select One
The complex number z1,z2andz3 satisfying z1−z3z2−z3=1−i√32,are the vertices of a triangle which is
Aof area zeroBright angled triangleCequilateralDobtuse angled triangle - Question 3 - Select One
The complex numbers z1,z2,z3 stisfying (z2=z3)=(1+i)(z1−z3).wherei=√−1, are vertices of a triangle which is
AequilateralBisoscelesCright angledDscalene
The complex numbers z1,=1+2i,z2=4−2iandz3=1−6i form the vertices of a (A) a right angled triangle (B) isosceles triangle (C) equilateral triangle (D) triangle whose one of the sides is of length 8
View Solutionlf z1,z2,z3 are the vertices of triangle such that |z1−i|=|z2−i|=|z3−i| and z1+z2=3i−z3 then area of triangle is
View SolutionIf |z|=2andz1−z3z2−z3=z−2z+2 , then prove that z1,z2,z3 are vertices of a right angled triangle.
View SolutionIf z1,z2,z3 are the vertices of an isoscles triangle right angled at z2, then
View SolutionIf z1,z2andz3 represent the vertices of an equilateral triangle such that
View Solution

