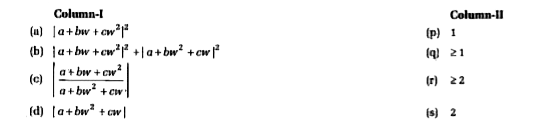The minimum value of , where a, b and c are all not equal integer and is a cube root of unity , is
1
0
The correct Answer is:C
Let
since a,b,c are all intergers but not all simulataneously equal
If a=b then
Because difference of intergerse = interger
and we have taken
From Eq.(i)
Hence minimum value of |Z| is 1
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY ( MATCH THE COLUMNS )
1 Videos
- COMPLEX NUMBERSBOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY ( FILL IN THE BLANKS )
2 Videos
- COMPLEX NUMBERSBOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 4 ROTATION OF A COMPLEX NUMBER (INTERGER ANSWER TYPE QUESTION )
1 Videos
- CIRCLEBOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 5 Integer Answer type Question
1 Videos
- DEFINITE INTEGRATIONBOOK - IIT JEE PREVIOUS YEARCHAPTER - DEFINITE INTEGRATIONEXERCISE - LIMITS AS THE SUM
6 Videos
Similar Questions
Knowledge Check
The minimum value of ∣∣a+bω+cω2∣∣, where a,b,c are all not equal integers and ω(≠1) is a cube root of unity, is
A√3B1/2C1D0If ω≠1 is a cube root of unity, then 1,ω,ω2
Aare vertices of an equilateral triangleBlie on a straight lineClie on a circle of radius √3/2DNone of theseIf ω is a cube root of unity but not equal to 1, then minimum value of ∣∣a+bω+cω2∣∣, (where a,b and c are integers but not all equal ), is
A0B√32C1D2
If p=a+bω+cω2, q=b+cω+aω2, and r=c+aω+bω2, where a,b,c≠0 and ω is the complex cube root of unity, then (a) p+q+r=a+b+c (b) p2+z2+r2=a2+b2+c2 (c) p2+z2+r2=−2(pq+qr+rp) (d) none of these
View SolutionLet ω≠1 be cube root of unity and S be the set of all non-singular matrices of the form ⎡⎢⎣1abω1cω2θ1⎤⎥⎦, where each of a,b,andc is either ω or ω2. Then the number of distinct matrices in the set S is (a) 2 (b) 6 (c) 4 (d) 8
View SolutionThe value of a+bω+cω2b+cω+aω2+a+bω+cω2c+aω+bω2 (where 'ω' is the imaginary cube root of unity), is (a) −ω (b). ω2 (c). 1 (d). −1
View SolutionIf p=a+bω+cω2,q=b+cω+aω2, and r=c+aω+bω2, where a,b,c≠0 and ω is the complex cube root of unity , then .
View SolutionIf ω is a cube root of unity but not equal to 1, then minimum value of ∣∣a+bω+cω2∣∣, (where a,b and c are integers but not all equal ), is
View Solution