The potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.Solution in Tamil
Step by step video & image solution for The potential energy function for a particle executing simple harmonic motion is given by V(x)=(1)/(2)kx^(2), where k is the force constant of the oscillatore. For k=(1)/(2)Nm^(-1), show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=+-2m. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:NCERT TAMILChapter:WORK, ENERGY AND POWERExercise:EXERCISES (ADDITIONAL EXERCISES)
Explore 7 Videos
- WORK, ENERGY AND POWERBook:NCERT TAMILChapter:WORK, ENERGY AND POWERExercise:EXAMPLE
Explore 36 Videos
- WORK, ENERGY AND POWERBook:NCERT TAMILChapter:WORK, ENERGY AND POWERExercise:EXERCISE - IV. NUMERICAL PROBLEMS
Explore 5 Videos
- WAVESBook:NCERT TAMILChapter:WAVESExercise:EVALUATION(IV. NUMERICAL PROBLEMS)
Explore 7 Videos
Similar Questions
A bullet of mass 0.012 kg and horizontal speed 70ms−1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by thin wire. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
View SolutionA box is pulled with a force of 25 N to produce a displacement of 15 m. If the angle between the force and displacement is 30∘, find the work done by the force.

View SolutionCalculate the work done by a force of 30 N in lifting a load of 2kg to a height of 10m (g=10ms−2)
View SolutionThe speed of a wave in a certain medium is 900 m/s. If 3000 waves passes over a certain point of the medium in 2 minutes, then compute its wavelength?
View SolutionThe potential energy function for a particle executing simple harmonic motion is given by V(x)=(1)/(2)kx^(2) , where k is the force constant of the oscillatore. For k=(1)/(2)Nm^(-1) , show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=+-2m.
View SolutionA particle moving along the X-axis executes simple harmonic motion, then the force acting on it is given by
where, A and K are positive constants.
View SolutionThe potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
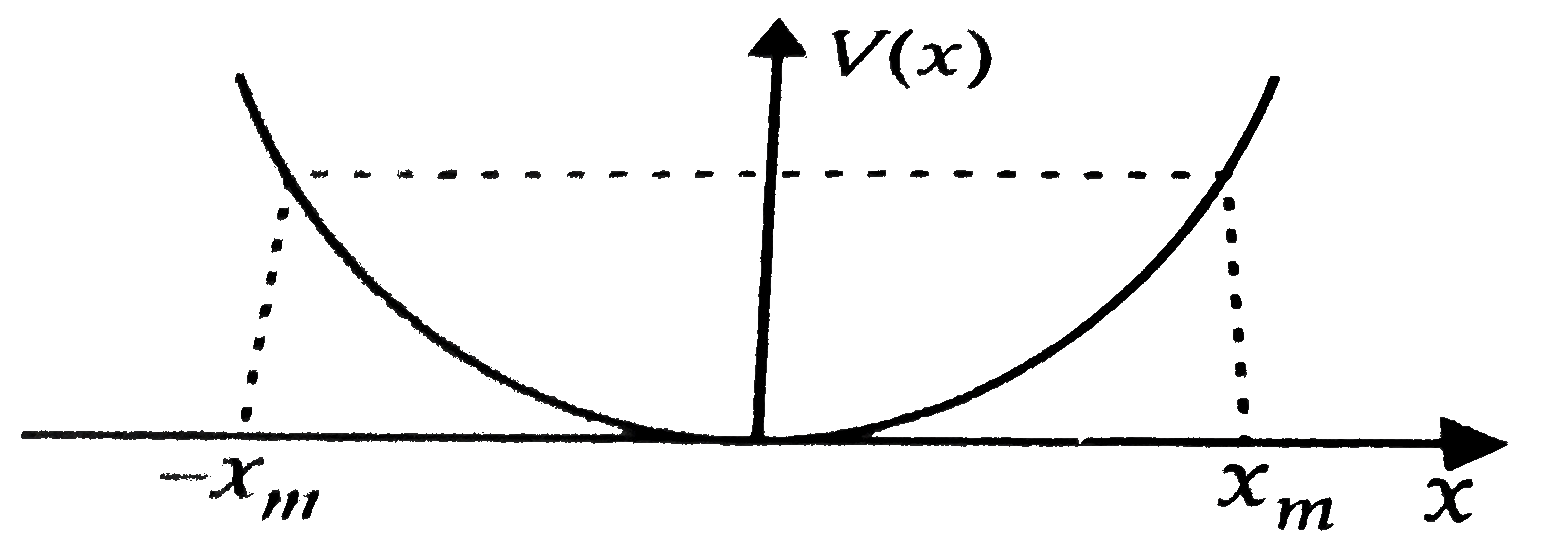
View Solutionरेखीय सरल आवर्त गति कर रहे किसी कण का स्थितिज ऊर्जा फलन V(x)12kx2 है, जहाँ k दोलन का बल नियतांक है। k=0।5Nm−1 के लिए V (x ) व x के मध्य ग्राफ चित्र में दिखाया गया है। यह दिखाइए की इस विभव के अंतर्गत गतिमान कुल 1 J ऊर्जा wale कण को अवश्य ही वापिस आना' चाहिए , अब यह x=±2 मीटर पर पहुँचता है।
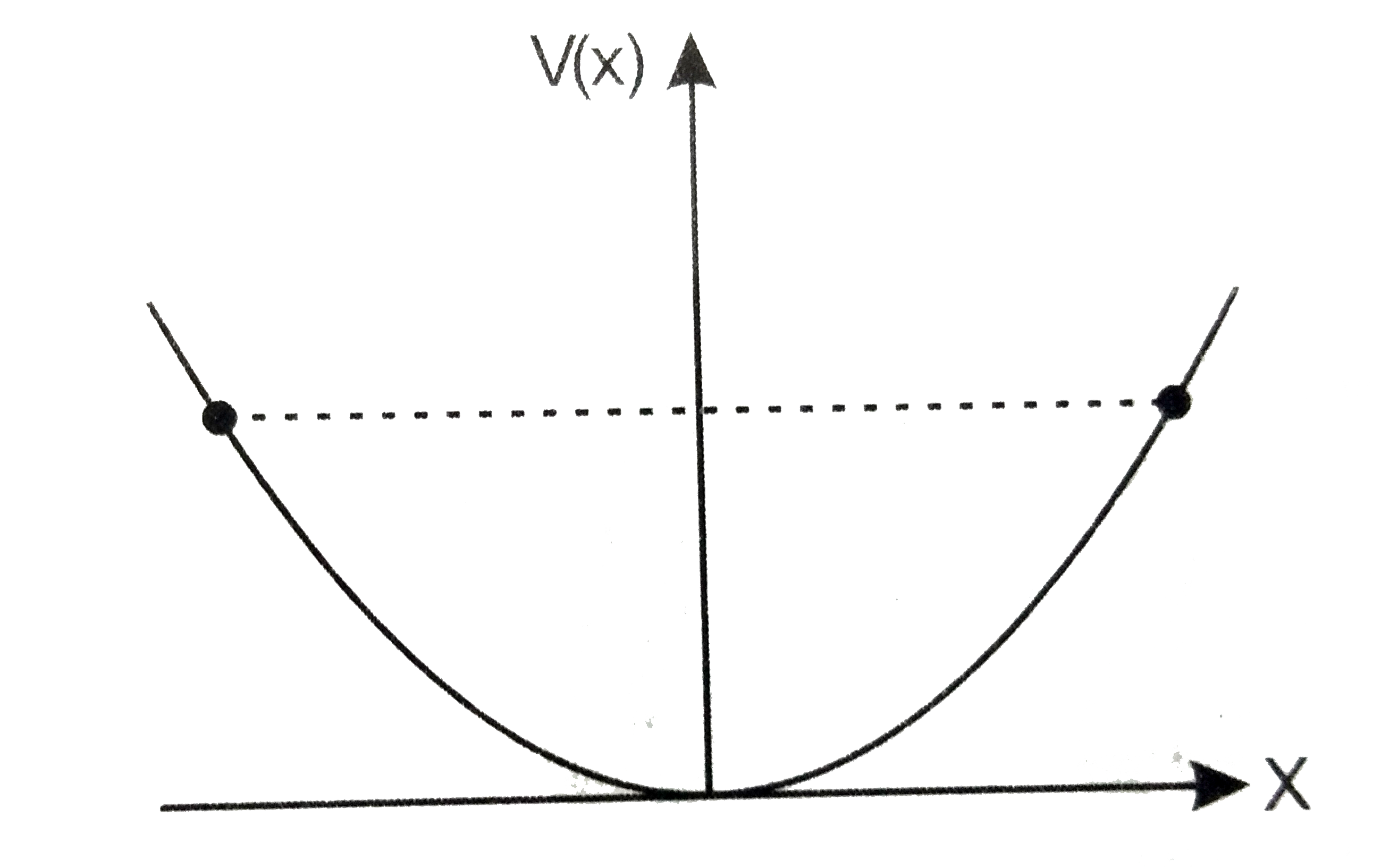
View SolutionThe potential energy of a particle in the X-Y plane is given by U=k(x+y), where 'k' is a constant. Find the amount of work done by the conservative force in moving a particle from (1, 1) to (2, 3).
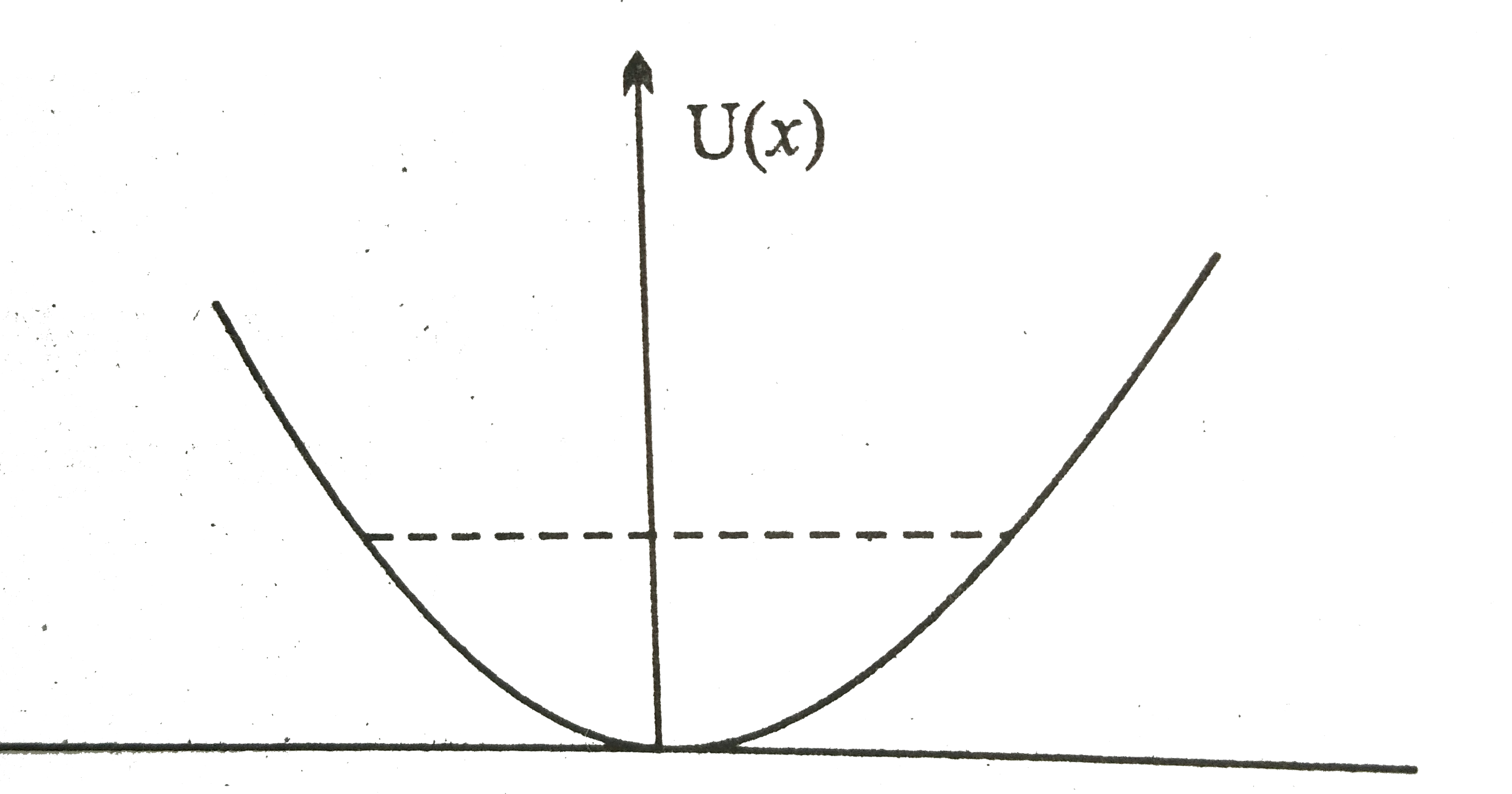
View Solutionरेखीय सरल आवर्त गति कर रहे किसी कण का स्थितिज ऊर्जा फलन U(x)=kx2/2 है, जहाँ k दोलक का बल नियतांक है । k=0.5Nm−1 के लिए U(x) व x के मध्य ग्राफ चित्र में दिखाया गया है । यह दिखाइए कि इस विभव के अंतर्गत गतिमान कुल 1J ऊर्जा वाले कण को अवश्य ही 'वापिस आना' चाहिए जब यह x=±2m पर पहुँचता है ।
View SolutionPotential energy of a particle is 12mω2x2, where m and ω are constants. Prove that the motion of the particle is simple harmonic.
View SolutionFor a particle executing simple harmonic motion, the kinetic energy K is given by,
K=K0cos2ωt
The maximum value of potential energy is :
View SolutionThe potential energy function for a particle executing linear simple harmonic motion is given by V(x)= kx^(2)"/"2 , where k is the force constant of the oscillator. For k= 0.5 Nm^(1) , the graph of V(x) versus x is shown in Fig. 6. 12. Show that a particle of total energy 1 J moving under this potential must 'turn back' when it reaches x= pm 2m .
View SolutionThe potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
View Solutionसरल रेखीय गति कर रहे किसी कण के लिए स्थितिज ऊर्जा फलन को V(x)=12kx2 के द्वारा निरूपित किया जाता है, जहाँ दोलित्र का बल गुणांक है। k=0.5Nm−1 के लिए, V(x) बनाम x के आरेख को चित्र में दर्शाया गया है। कुल ऊर्जा E का कण उस समय वापस हो जाता है जब यह x=±xm पर पहुँचता है। यदि x=±xm पर किसी कण की स्थितिज व गतिज ऊर्जा को क्रमश: V व K के द्वारा दर्शाया जाता है, तब निम्न में से कौन-सा सही है?
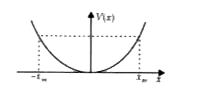
View SolutionThe potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
View Solution
