The potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
To solve the problem, we will follow these steps:
Step 1: Understand the Energy Conservation Principle
The total mechanical energy E of a particle in simple harmonic motion is the sum of its kinetic energy K and potential energy V:
E=K+V
Given that the total energy E is 1 joule, we can express this as:
1 J=K+V
Step 2: Write the Expression for Potential Energy
The potential energy V for a particle executing simple harmonic motion is given by:
V(x)=12kx2
where k is the force constant. We are given k=12N/m.
Step 3: Substitute the Values into the Potential Energy Equation
Substituting k into the potential energy equation, we have:
V(x)=12(12)x2=14x2
Step 4: Calculate the Potential Energy at x=±2m
Now, we will calculate the potential energy when x=2m (the same value will apply for x=−2m):
V(2)=14(2)2=14⋅4=1 J
Step 5: Set Up the Energy Equation
At the turning points x=±2m, the kinetic energy K must be zero because the particle is momentarily at rest. Therefore, we can set up the equation:
E=K+V⇒1 J=0+V(2)
Step 6: Conclude that the Particle Must Turn Back
Since we found that V(2)=1 J, we can substitute back into the energy equation:
1 J=0+1 J
This implies that at x=±2m, the kinetic energy is zero, meaning the particle cannot continue moving in that direction and must turn back.
Final Conclusion
Thus, we have shown that the particle must turn back when it reaches x=±2m.
---
The total mechanical energy E of a particle in simple harmonic motion is the sum of its kinetic energy K and potential energy V:
E=K+V
Given that the total energy E is 1 joule, we can express this as:
1 J=K+V
The potential energy V for a particle executing simple harmonic motion is given by:
V(x)=12kx2
where k is the force constant. We are given k=12N/m.
Substituting k into the potential energy equation, we have:
V(x)=12(12)x2=14x2
Now, we will calculate the potential energy when x=2m (the same value will apply for x=−2m):
V(2)=14(2)2=14⋅4=1 J
At the turning points x=±2m, the kinetic energy K must be zero because the particle is momentarily at rest. Therefore, we can set up the equation:
E=K+V⇒1 J=0+V(2)
Since we found that V(2)=1 J, we can substitute back into the energy equation:
1 J=0+1 J
This implies that at x=±2m, the kinetic energy is zero, meaning the particle cannot continue moving in that direction and must turn back.
Thus, we have shown that the particle must turn back when it reaches x=±2m.
Topper's Solved these Questions
Similar Questions
The total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.
View SolutionThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
View Solution
Knowledge Check
The potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
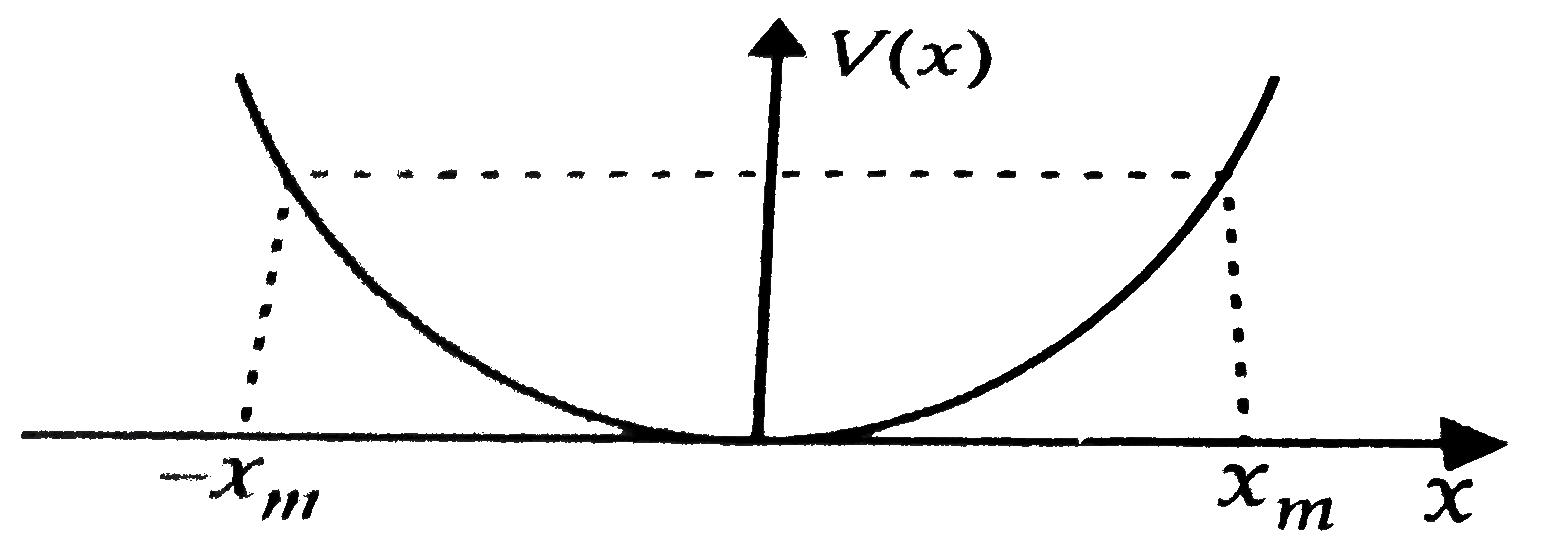 AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt EConsider the following statements. The total energy of a particles executing simple harmonic motion depends on its
1. amplitude
2. Period
3. displacement of these :A1 and 2 are correctB2 and 3 are correctC1 and 3 are correctD1, 2 and 3 are correct
The potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionThe potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[x22−x]J. If total mechanical speed (in m/s):-
View SolutionThe potential energy of particle of mass 1kg moving along the x-axis is given by U(x)=16(x2−2x) J, where x is in meter. Its speed at x=1 m is2m/s. Then,
View SolutionTotal energy of a particle executing oscillating motionis 3 joule and given by
E=x2+2x+v2−2v
Where x is the displacement from origin at x=0 and v is velocity of particle at x. Then choose the correct statements)
View SolutionA particle moving along the X-axis executes simple harmonic motion, then the force acting on it is given by
where, A and K are positive constants.
View SolutionThe potential energy of a particle of mass m is given by U=12kx2 for x<0 and U = 0 for x≥0. If total mechanical energy of the particle is E. Then its speed at x=√2Ek is
View Solution
