The potential energy function for a particle executing linear simple harmonic motion is given $U (x) = \frac{1}{2} k x^{2}$ , where k is the force constant of the oscillator. For k=0.5 $N m^{- 1}$ , the graph of U(x) on Y-axis x is shown figure. The particle has total energy 1J. Moving this potential it turns back when it reaches $x = \pm$ _________m

Text Solution

Verified by Experts

The correct Answer is:2

Updated on:21/07/2023

The potential energy function for a particle executing linear SHM is given by $V (x) = \frac{1}{2} k x^{2}$ where k is the force constant of the oscillator. For $k = 0.5 N m^{- 1}$ , the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches $x = \pm x_{m}$ .if V and K indicate the potential energy and kinetic energy respectively of the particle at $x = + x_{m}$ ,then which of the following is correct?

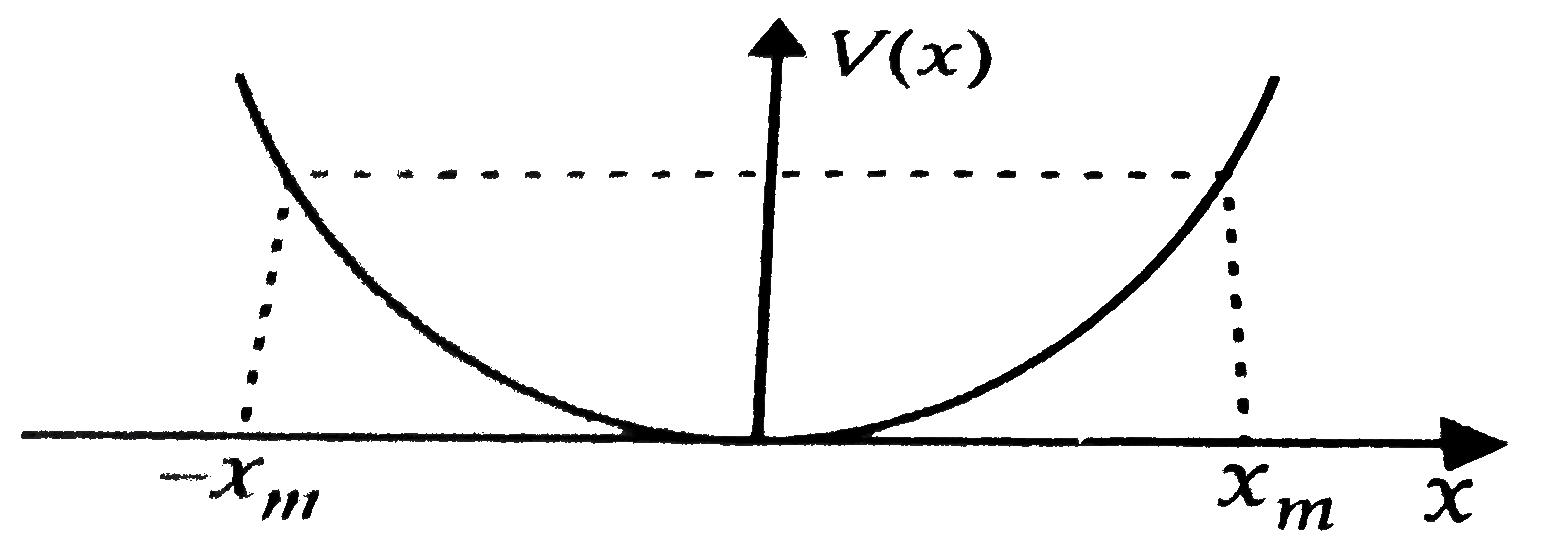AV=0, K=E
BV=E, K=0
CV lt K, K=0
DV=0, K lt E
The potential energy function for a particle executing linear SHM is given by $V (x) = \frac{1}{2} k x^{2}$ where k is the force constant of the oscillator. For $k = 0.5 N m^{- 1}$ , the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches $x = \pm x_{m}$ .if V and K indicate the potential energy and kinetic energy respectively of the particle at $x = + x_{m}$ ,then which of the following is correct?

AV=0, K=E
BV=E, K=0
CV lt K, K=0
DV=0, K lt E
The potential energy of a particle executing SHM along the x-axis is given by $U = U_{0} - U_{0} cos a x$ . What is the period of oscillation?
A $2 π \sqrt{\frac{m a}{U_{0}}}$
B $2 π \sqrt{\frac{U_{0}}{m a}}$
C $\frac{2 π}{a} \sqrt{\frac{m}{U_{0}}}$
D $2 π \sqrt{\frac{m}{a U_{0}}}$