A tank with a square base of area 1.0m2 is divided by a vertical parition in the middle. The bottom of the partition has a small hinged door of area 20cm2. The tank is filled with water and an acid (of relative density 1.7) in the other, both to a height of 4.0m. Compute to force necessary the force nec cessary to keep the door closed.Solution in Tamil
55 N (note the base area does not affect the answer)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS Book:NCERT TAMILChapter:MECHANICAL PROPERTIES OF FLUIDS Exercise:EXERCISE
Explore 45 Videos
- LAWS OF MOTIONBook:NCERT TAMILChapter:LAWS OF MOTIONExercise:EXERCISE (V. Numerical Problems)
Explore 14 Videos
- MECHANICAL PROPERTIES OF SOLIDS Book:NCERT TAMILChapter:MECHANICAL PROPERTIES OF SOLIDS Exercise:Exercises
Explore 21 Videos
Similar Questions
Why the blood pressure in humans is greater at the feet than at the brain?
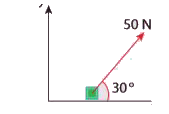
View SolutionA force of 50N act on the object of mass 20 kg. shown in the figure. Calculate the acceleration of the object in x and y directions
View SolutionA steel wire of length 4.5 m and cross-sectional area 3×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 1x10−5m2 under a given load. The ratio of the Young's modulus of steel to that of copper is
View SolutionA tank with a square base of area 2m^2 is divided into two compartments by a vertical partition in the middle. There is a small hinged door of face area 20 cm^2 at the bottom of the partition. Water is filled in one compartment and an of the partition. Water is filled in one compartment and an acid fo relvative density 1.5 in the other, both to a height of 4m. The force necassary to keep the door closed is (Take g = 10 m s^(-2))
View SolutionA tank with a square base of area 1.0m^(2) is divided by a vertical parition in the middle. The bottom of the partition has a small hinged door of area 20cm^(2) . The tank is filled with water and an acid (of relative density 1.7) in the other, both to a height of 4.0m . Compute to force necessary the force nec cessary to keep the door closed.
View Solution1.0m2 क्षेत्रफल के वर्गाकार आधार वाले किसी टैंक को बीच में ऊर्ध्वाधर विभाजक दीवार द्वारा दो भागों में बांटा गया हैं। विभाजक दीवार में नीचे 20cm2 क्षेत्रफल का कब्जेदार दरवाजा हैं। टैंक का एक भाग जल से भरा हैं तथा दूसरा भाग 1.7 आपेक्षिक घनत्व के अम्ल से भरा हैं। दोनों भाग 4.0 m ऊंचाई तक भरे गए हैं। दरवाजें को बंद रखने के आवश्यक बल परिकलित कीजिये।
View Solution1.0m2 क्षेत्रफल के वर्गाकार आधार वाले किसी टैंक को बीच में ऊर्ध्वाधर विभाजक दीवार द्वारा दो भागो में बाँटा गया है । विभाजक दीवार में नीचे 20cm2 क्षेत्रफल का कब्जेदार दरवाजा है । टैंक का एक भाग जल से भरा है तथा दूसरा भाग 1.7 आपेक्षिक घनत्व के अम्ल से भरा है । दोनों भाग 4.0m ऊँचाई तक भरे गए है । दरवाजे को बंद रखने के आवश्यक बल परिकलित कीजिए ।
View Solution1.0 मीटर 2 क्षेत्रफल के वर्गाकार आधार वाले किसी टैंक के बिच में ऊर्ध्वधर विभाजक दीवार द्वारा दो भागों में बांटा गया है । विहभाजक दिवार में निचे 20 सेमि 2 क्षेत्रफल का कब्जेदार दरवाजा है टेंक का एक भाग जल से भरा है तथा दूसरा भाग 1.7 आपेक्षिक घनत्व के अम्ल से भरा है | दोनों भाग 4.0 मीटर ऊंचाई तक भरे गए है दरवाजे को बंद रखने के आवश्यक बल परिकलित कीजिए
(##BLJ_HIN_PHY_XI_C16_E07_035_Q01.png" width="80%">
View SolutionA tank with a square base of area 1.0m^(2) is divided by a vertical partition in the middle. The bottom of the partition has a small-hinged door of area 20cm^(2) . The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other, both to a height of 4.0 m. Compute the force necessary to keep the door closed.
View SolutionA tank with a square base of area 1.0m2 is divided by a vertical position in the middle. The bottom of the partition has a small hinged door of area 20cm2 The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other. both to the height of 4.0 cm compute the force necessary to keep the door close.
View SolutionA tank with a square base of area 1.0m2 is divided by a vertical position in the middle. The bottom of the partition has a small hinged door of area 20cm2 The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other. both to the height of 4.0 cm compute the force necessary to keep the door close.
View SolutionA tank with a square base of area 1.0 m^2 is divided by a vertical position in the middle. The bottom of the partition has a small hinged door of area 20 cm^2 The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other. both to the height of 4.0 cm compute the force necessary to keep the door close.
View SolutionA tank with a square base of area 1.0m2 is divided by a vertical position in the middle. The bottom of the partition has a small hinged door of area 20cm2 The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other. both to the height of 4.0 cm compute the force necessary to keep the door close.
View SolutionA tank with a square base of area 1.0m^(2) is divided by a vertical parition in the middle. The bottom of the partition has a small hinged door of area 20cm^(2) . The tank is filled with water and an acid (of relative density 1.7) in the other, both to a height of 4.0m . Compute to force necessary the force nec cessary to keep the door closed.
View SolutionA tank with a square base of area 1.0m2 is divided by a vertical partition in the middle The bottom of the partition has a small - hinged door of area 20cm2 . The tank is filled with water in one compartement , and and an acid (of relative density 1.7) in the other , both to a height of 4.0 m . compute the force necessary to keep the door close.

View SolutionA tank with a square base of area 2m^2 is divided into two compartments by a vertical partition in the middle. There is a small hinged door of face area 20 cm^2 at the bottom of the partition. Water is filled in one compartment and an acid of relative density 1.5 in the other, both to a height of 4m. The force necessary to keep the door closed is (Take g = 10 m s^(-2))
View Solution
