A tank with a square base of area 1.0m2 is divided by a vertical parition in the middle. The bottom of the partition has a small hinged door of area 20cm2. The tank is filled with water and an acid (of relative density 1.7) in the other, both to a height of 4.0m. Compute to force necessary the force nec cessary to keep the door closed.
To solve the problem step by step, we will calculate the force necessary to keep the hinged door closed at the bottom of the tank.
Step 1: Identify the given data
- Area of the tank base, A=1.0m2
- Area of the hinged door, a=20cm2=20×10−4m2
- Height of both liquids, h=4.0m
- Density of water, ρ1=103kg/m3
- Relative density of acid = 1.7, so density of acid, ρ2=1.7×103kg/m3
- Acceleration due to gravity, g=9.8m/s2
Step 2: Calculate the pressure exerted by the water
The pressure exerted by the water at the bottom of the tank can be calculated using the formula:
P1=h⋅ρ1⋅g
Substituting the values:
P1=4.0m⋅(103kg/m3)⋅(9.8m/s2)=3.92×104Pa
Step 3: Calculate the pressure exerted by the acid
Similarly, the pressure exerted by the acid is given by:
P2=h⋅ρ2⋅g
Substituting the values:
P2=4.0m⋅(1.7×103kg/m3)⋅(9.8m/s2)=6.66×104Pa
Step 4: Calculate the pressure difference
The pressure difference (ΔP) between the acid and the water is:
ΔP=P2−P1
Substituting the values:
ΔP=(6.66×104Pa)−(3.92×104Pa)=2.744×104Pa
Step 5: Calculate the force required to keep the door closed
The force (F) necessary to keep the door closed can be calculated using the formula:
F=ΔP⋅a
Substituting the values:
F=(2.744×104Pa)⋅(20×10−4m2)=54.88N
Final Answer
The force necessary to keep the door closed is approximately 54.88N.
- Area of the tank base, A=1.0m2
- Area of the hinged door, a=20cm2=20×10−4m2
- Height of both liquids, h=4.0m
- Density of water, ρ1=103kg/m3
- Relative density of acid = 1.7, so density of acid, ρ2=1.7×103kg/m3
- Acceleration due to gravity, g=9.8m/s2
The pressure exerted by the water at the bottom of the tank can be calculated using the formula:
P1=h⋅ρ1⋅g
Substituting the values:
P1=4.0m⋅(103kg/m3)⋅(9.8m/s2)=3.92×104Pa
Similarly, the pressure exerted by the acid is given by:
P2=h⋅ρ2⋅g
Substituting the values:
P2=4.0m⋅(1.7×103kg/m3)⋅(9.8m/s2)=6.66×104Pa
The pressure difference (ΔP) between the acid and the water is:
ΔP=P2−P1
Substituting the values:
ΔP=(6.66×104Pa)−(3.92×104Pa)=2.744×104Pa
The force (F) necessary to keep the door closed can be calculated using the formula:
F=ΔP⋅a
Substituting the values:
F=(2.744×104Pa)⋅(20×10−4m2)=54.88N
The force necessary to keep the door closed is approximately 54.88N.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE
31 Videos
- LAWS OF MOTION BOOK - NCERT ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EXERCISE
40 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
21 Videos
Similar Questions
A tank, with a square base of area 1.0m2 is divided by a vertical partition has a small hinged door of aren 20cm2. The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other, both to the height of 4.0 m. Compute the force necessary to keep the door closed
View SolutionWater flows into a large tank with flat bottom at the rate of 10−4m3s−1. Water is also leaking out of a hole of area 1 cm2 at its bottom. If the height of the water in the tank remains steady, then this height is :
View Solution
Knowledge Check
A tank with a square base of area 2m2 is divided into two compartments by a vertical partition in the middle. There is a small hinged door of face area 20cm2 at the bottom of the partition. Water is filled in one compartment and an acid of relative density 1.5 in the other, both to a height of 4m. The force necessary to keep the door closed is (Takeg=10ms−2)
A10NB20 NC40 ND80 N
A rectangular tank of base area 100 m2 has a height of 2 m. Calculate the thrust at the bottom of the tank, if it is filled upto the brim with water of density 103 kg m−3.
View SolutionThe wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,
,
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
The total force exerted by all the fluids on the conical cork in the vertical direction is
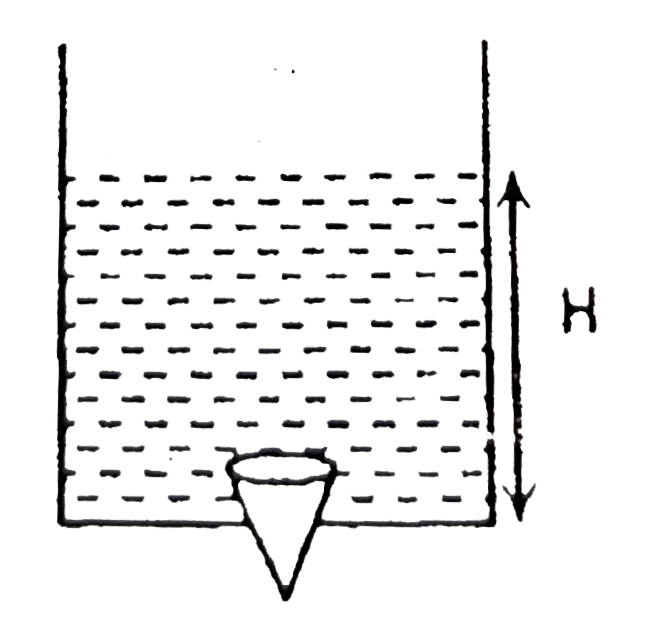
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
Calculate the force exerted by water on the curved surface of the conical cork submerged in water when the liquid level in the vessel is equal to H.
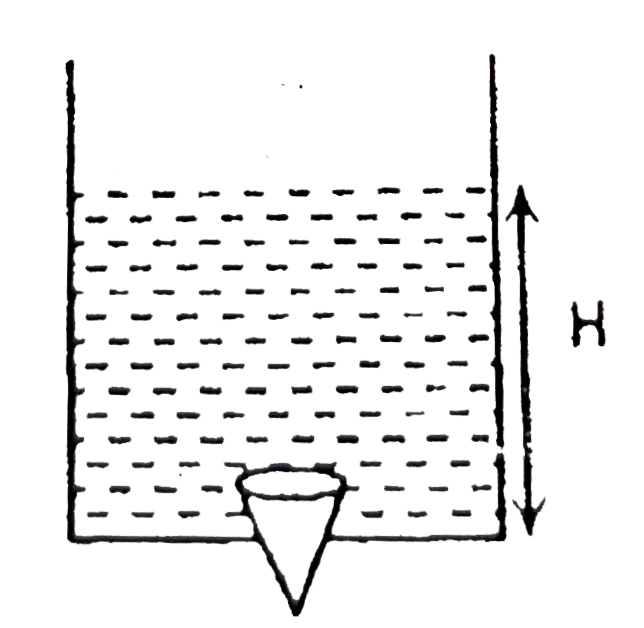
View Solution
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionWater is filled in a rectangular tank of size 3m×2m×1m. a) Find the total force exerted by the water on the bottom surface of the tank. b) Consider a vertical side of area 2m×1m. Take a horizontal strip of wide δx metre in this side, situated at a depth of x metre from the surface of water.Find the force by the water on this strip. c) Find the torque of the force calculate in part b) about the bottom edge of this side. d) Find the total force by the water on this side. e) Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take =10ms−2.
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
Calculate the value of H.
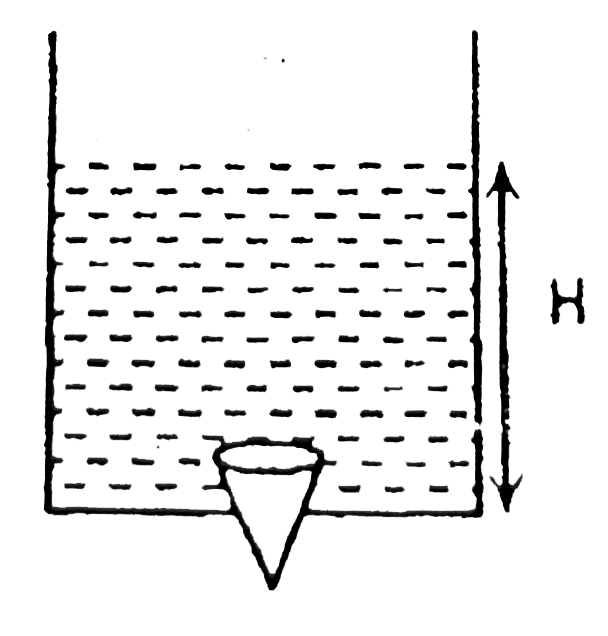
View Solution
