A parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after . (The charge on the capacitor at time t is q (t) = CV [1 – exp ], where the time constant is equal to CR.)
![A parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R = 1 M Omega across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t = 10^(-3) s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t// tau)], where the time constant tau is equal to CR.)](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_TEL_PHY_XII_P1_C08_SLV_001_Q01.png) Solution in Telugu
Solution in Telugu
The time constant of the CR circuit is . Then, we have
The electric field in between the plates at time t is
= area of the plates.
Consider now a circular loop of radius (1/2) m parallel to the plates passing through P. The magnetic field B at all points on the loop is along the loop and of the same value. The flux through this loop is
area of the loop
The displacement current
at . Now, applying Ampere-Maxwell law to the loop, we get
or,
Similar Questions
एक समांतर प्लेट संधारित्र जिसकी वृताकार प्लटो की त्रिज्या 1m है धारिता 1nF है समय t =0 पर इसको आवेशित करने के लिए R=1MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में 2V की बैटरी से जोड़ा गया है ( चित्र ) 10−3S के पश्चात संधारित्र के बीच में दोनों प्लेटो के केंद्र एवं परिकलन कीजिए [क्षण t पर संधारित्र पर आवेश q(t)=CV[1−exp(−t/t) होता है जहाँ समय नियतांक τ=CR है
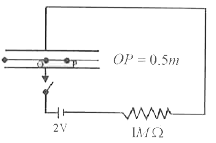
View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 1nF. At t = 0, it is connected for chargeing in series with a resistor R=1 M Omega across a 2V battery (Figure). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10^(-3)s . (The charge on the capacitor at time t is q(t)=CV[1-exp((-t)/(tau))] , where the time constant tau is equal to CR).
View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)

View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)
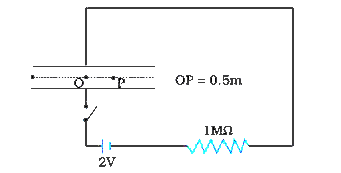
View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitor of 1nF. At t=0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery. Calculate the magnetic field at a point P, halfway between the cnetre and the periphery of the plates, after t=10−3sec.
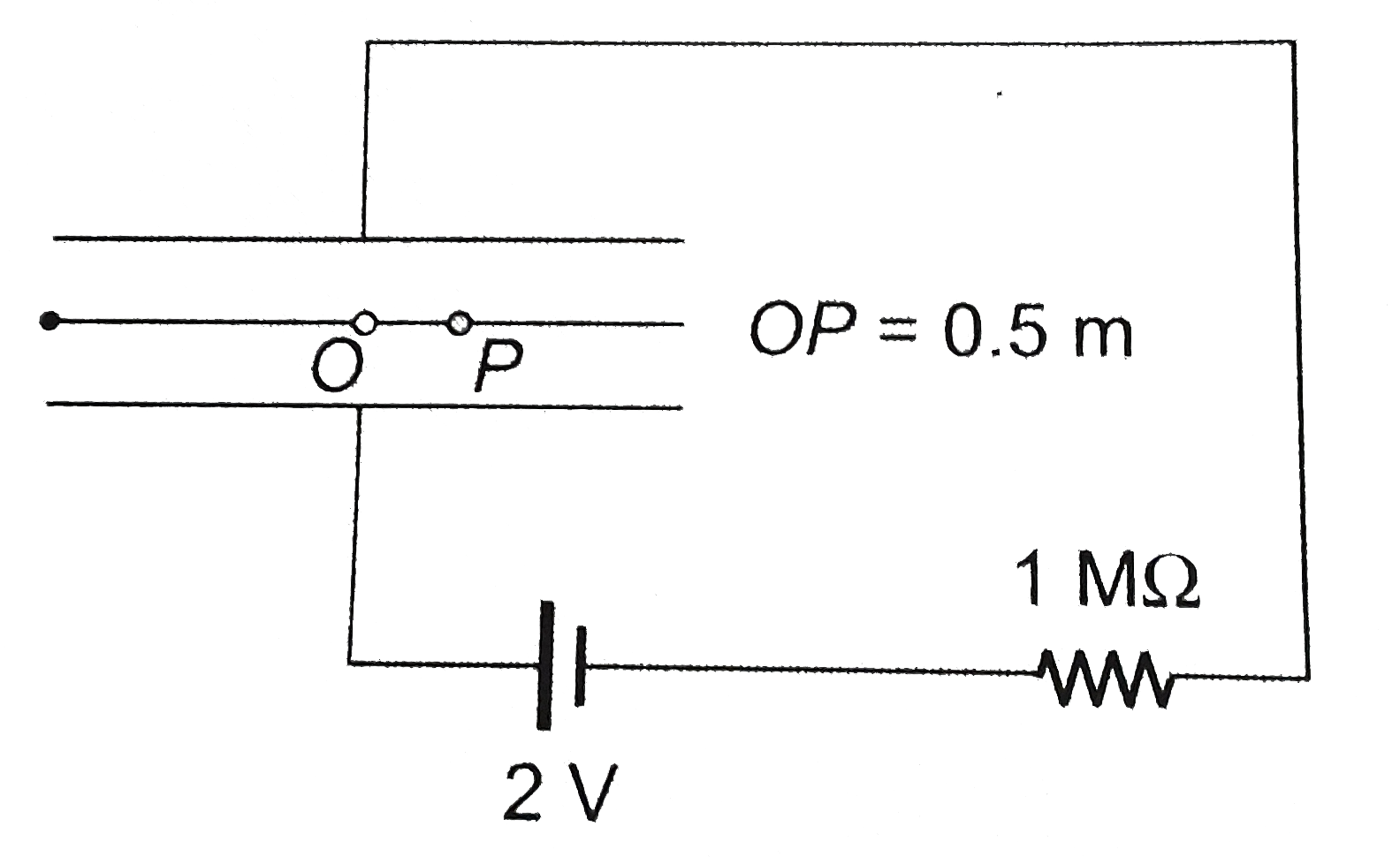
View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MO¬a across a 2V battery. Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 - exp (−t/τ)], where the time constant τ is equal to CR.)

View SolutionA parallel plate capacitor with circular plates of radius 0.8 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R = 1 M Omega across a 4V battery. Calculate the magnetic field at a point P, halfway between the centre and the perpendicular of the plates after t=10^(-3)s . (The charge on the capacitor at time t is q (t) = CV [1 - exp (-t//tau) ], where the time constant tau is equal to CR.)
View Solution
