A massless rod of length L has two equal charges (q) tied to its ends. The rod is free to rotate in horizontal plane about a vertical axis passing through a point at a distance from one of its ends. A uniform horizontal electric field (E) exists in the region. (a) Draw diagrams showing the stable and unstable equilibrium positions of the rod in the field. (b) Calculate the change in electric potential energy of the rod when it is rotated by an angle from its stable equilibrium position. (c) Calculate the time period of small oscillations of the rod about its stable equilibrium position. Take the mass of each charge to be m.
The correct Answer is:(b).
(c)
Step by step video, text & image solution for A massless rod of length L has two equal charges (q) tied to its ends. The rod is free to rotate in horizontal plane about a vertical axis passing through a point at a distance (L)/(4) from one of its ends. A uniform horizontal electric field (E) exists in the region. (a) Draw diagrams showing the stable and unstable equilibrium positions of the rod in the field. (b) Calculate the change in electric potential energy of the rod when it is rotated by an angle Deltatheta from its stable equilibrium position. (c) Calculate the time period of small oscillations of the rod about its stable equilibrium position. Take the mass of each charge to be m. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
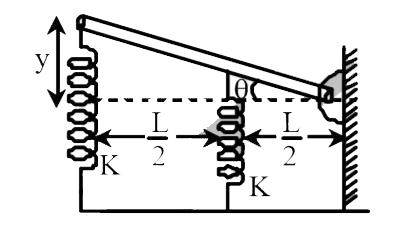
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L3 from one of its ends and perpendicular to the rod is
View Solution
Knowledge Check
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotationThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L3 from one of its ends and perpendicular to the rod is
A748ML2BML29CML212DML22The radius of gyration of rod of length L and mass M about an axis perpendicular to its length and passing through a point at a distance L/3 from one of its ends is
A√76LBL29CL3D√52L
The moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View SolutionThere is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it at a L/4 distance from one of its ends.
What is the time period of the SHM as mentioned in previous question?
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionThere is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it at a L/4 distance from one of its ends.
In what position is the rod to be set so that if displaced a little from that position it begins a hormonic oscillation about the axisA?
View Solution
