The heaviest and lightest strings on a certain violin have linear densities of 3.2 and 0.26 g/m. What is the ratio of the diameter of the heaviest string to that of the lightest string, assuming that the strings are of the same material?
The correct Answer is:3.5
Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Single Correct Choice Type)
33 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (More than One Coorect Choice Type)
10 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Checkpoint
8 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
Two strings of same material are joined to form a large string and is stretched between rigid supports. The diameter of the second string is twice that of the first. It was observed in an experiment that the whole string was oscillating in 4 loops with a node at the joint. Find the possible lengths of the second string if the length of first string is 90 cm.
View SolutionStatement-1 : Strings of a guitar have different diameters.
Statement-2 : String with least diameter produce the lower notes.
View Solution
Knowledge Check
The linear mass density μ of the string is (where, mass of the string = m, length, of the string g = L)
AmLBmLCmL2DmL3The linear mass density 'μ' of the string is (where, mass of the string = m, length of the string = L)
AmLBmLCmt2DmL3A string of length 0.5m and linear density 10−4 kg/m is stretched under a tension of 100 N. If the frequency of the vibration of the string is 4000 Hz, how many loops are formed on the string?
A1B4C2D6
A bird with mass m parches at the middle of a strectched string Show that the tension in the string is give by T=mg2sinθ. Assuming that each half of the string is straight.

View SolutionA bird with mass m parches at the middle of a strectched string Show that the tension in the string is give by T=mg2sinθ. Assuming that each half of the string is straight.

View SolutionTransverse waves pass through the strings A and B attached to an object of mass m as shown. If μ is the linear density of each of the strings the velocity of the transverse waves produced in the strings A and B is
View SolutionTransverse waves pass through the strings A and B attached to an object of mass 'm' as shown. If μ is the linear density of each of the strings, the velocity of the transverse waves produced in the strings A and B is
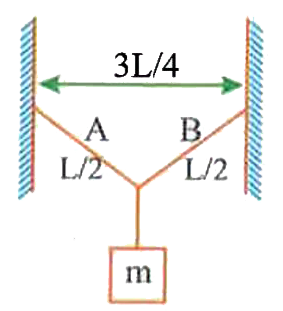
View SolutionThere are two strings of same material same diameter and length l and 2l stretched under same tension . If the strings are plucked and released, velocities of transverse waves on the two strings will be in the ratio
View Solution
