Two waves are generated on a string of length 4.0 m to produce a three-loop standing wave with an amplitude of 1.0 cm.The wave speed is 100 m/s. Let the equation for one of the waves be of the form y(x,t)=ymsin(kx+ωt). In the equation for the other wave, what are (a) ym (b) k, (c) ω and (d) the sign in front of w!
The correct Answer is:(a) 5.0×10−3m,(b)2.4m−1;(c)38Hz; (d) minus
Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Single Correct Choice Type)
33 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (More than One Coorect Choice Type)
10 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Checkpoint
8 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
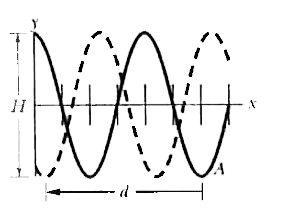
Two sinusoidal waves with the same amplitude and wavelength travel through each other along a string that is stretched along an x axis. Their resultant wave is shown twice in Fig. 16-53, as the antinode A travels from an extreme upward displacement to an extreme downward displacement in 6.0 ms. The tick marks along the axis are separated by 15 cm, height H is 1.20 cm. Let the equation for one of the two waves be of the form y(x,t)=ymsin(kx+ω). In the equation for the other wave, what are (a)ym(b)k,(c)ω, and (d) the sign in front of ω?

View SolutionTwo sinusoidal waves with the same amplitude of 6.00 mm and the same wavelength travel together along a string that is stretched along an x axis. Their resultant wave is shown twice in Fig. 16 39. as velley travels in the negative direction of the x axis by distance d= 56.0 cm in 8.0 ms. The lick matks along the axis are separated by 10cm, and height H is 8.0mm. Let the equation for one wive be of the form y(x,t) =ymsin(kx±ωt+ϕ1), where ϕ1=0 and you must choose the correct sign in front of ω. For the equation for the other wave, what are (a) ym,(b)k,(c)ω,(d)ϕ2, and (e) the sign in front of ω?
View Solution
Knowledge Check
y=acos(kx+ωt) superimposes on another wave giving a stationary wave having node at x = 0. What is the equation of the other wave
A−acos(kx+ωt)Bacos(kx−ωt)C−acos(kx−ωt)D−asin(kx+ωt)A wave represented by the equation y=acos(kx−ωt) is superposed with another wave to form stationary wave such that the point x=0 is a node. The equation for the other wave is:
Aasin(kx+ωt)B−acos(kx−ωt)C−acos(kx−ωt)D−asin(kx−ωt)
A stretched string has a mass per unit length of 5.00 g/cm and a tension of 10.0 N A sinusoidal wave on this string has an amplitude of 0.16 mm and a frequency of 100 Hz and is traveling in the negative direction of an x axis. If the wave equation is of the form y(x,t)= ymsin(kx±ωt), what are (a) ym (b) k. (c) ω, and (d) the correct choice of sign in front of ω?
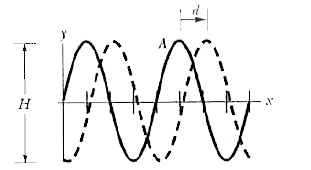
View SolutionIn Fig 16-46, a sinusoidal wave moving along a string is shown twice as crest A travels in the positive direction of any x axis by distance d=6.0 cm in 3.0 ms. The tick marks along the axis are separated by 10cm, height H=6.00MM. The equation for the wave is in the form y(x,t) =ymsin(kx±ωt). so what are (a) ym,(b)k,(c)ω and (d) the correct choice of sign in front of ω?
View SolutionA transverse sinusoidal wave is moving along a string in the opposite direction of an x axis with a speed of 70m/s. At t=0 the string particle at x=0 has a transverse displacement of 4.0 cm and is not moving. The maximum transverse speed of the string particle at x=0 is 16m/s. (a) What is the frequency of the wave? (b) What is the wavelength of the wave? If y(x,t) =ymsin(kx±ωt+ϕ) is the form of the wave equation, what are (c) ym,(d)k,(e)ω(f)ϕ, and (g) the correct of sign in front of ω?
View SolutionA standing wave pattern is formed on a string One of the waves if given by equation y1=acos(ωt−kx+π3) then the equation of the other wave such that at x=0 a node is formed.
View SolutionA standing wave pattern is formed on a string One of the waves if given by equation y1=acos(ωt−kx+π3) then the equation of the other wave such that at x=0 a node is formed.
View SolutionA standing wave pattern is formed on a string.One of the waves is given by equation y1=acos(ωt−kx+π3) ,then the equation of the other wave such that x=0 a node is formed is-
View Solution
