The total energy of molecules is divided equally amongst the various degrees of freedom of a molecule. The distribution of kinetic energy along x, y, z axis are EKx,EKy,EKz
Total K.e =EKx+EKy+EKz
Since the motion of molecule is equally probable in all the three directions, therefore
EKx=EKy=EKz=13EK=13×32kT=12kT, where k=RNA = Botzman constant.
K.E.=12kT per molecule or =12RT per mole.
In vibration motion, molecules possess both kinetic energy as well as potential energy. This means energy of vibration involves two degrees of fiuedom.
Vibration energy =2×12kT=2×12RT [∴ two degrees of freedom per mole]
If the gas molecules have n1 translational degrees of freedom, n2 rotational degrees of freedom and n3 vibrational degrees of freedom, that total energy = n1[kT2]+n2[kT2]+n3[kT2]×2
![The total energy of molecules is divided equally amongst the various degrees of freedom of a molecule. The distribution of kinetic energy along x, y, z axis are E(K(x)), E(K(y)), E(K(z)) Total K.e =E(K(x)) + E(K(y)) + E(K(z)) Since the motion of molecule is equally probable in all the three directions, therefore E(K(x)) = E(K(y)) = E(K(z)) =1/3 E(K) =1/3 xx 3/2 kT = 1/2 kT, where k =R/N(A) = Botzman constant. K.E. = 1/2 kT per molecule or =1/2 RT per mole. In vibration motion, molecules possess both kinetic energy as well as potential energy. This means energy of vibration involves two degrees of fiuedom. Vibration energy =2 xx 1/2kT =2 xx 1/2RT [therefore two degrees of freedom per mole] If the gas molecules have n(1) translational degrees of freedom, n2 rotational degrees of freedom and n(3) vibrational degrees of freedom, that total energy = n(1)[(kT)/2] + n(2) [(kT)/2] + n(3) [(kT)/2] xx 2 Where 'n' is atomicity of gas. The rotational kinetic energy of H20 molecule is equal to](https://d10lpgp6xz60nq.cloudfront.net/physics_images/AKS_AO_CHE_V01_P2_C02_E02_087_Q01.png)
Where 'n' is atomicity of gas.
The rotational kinetic energy of H20 molecule is equal toSolution in Telugu
32kT
12kT
kT
2kT
The correct Answer is:A
Step by step video, text & image solution for The total energy of molecules is divided equally amongst the various degrees of freedom of a molecule. The distribution of kinetic energy along x, y, z axis are E_(K_(x)), E_(K_(y)), E_(K_(z)) Total K.e =E_(K_(x)) + E_(K_(y)) + E_(K_(z)) Since the motion of molecule is equally probable in all the three directions, therefore E_(K_(x)) = E_(K_(y)) = E_(K_(z)) =1/3 E_(K) =1/3 xx 3/2 kT = 1/2 kT, where k =R/N_(A) = Botzman constant. K.E. = 1/2 kT per molecule or =1/2 RT per mole. In vibration motion, molecules possess both kinetic energy as well as potential energy. This means energy of vibration involves two degrees of fiuedom. Vibration energy =2 xx 1/2kT =2 xx 1/2RT [therefore two degrees of freedom per mole] If the gas molecules have n_(1) translational degrees of freedom, n_2 rotational degrees of freedom and n_(3) vibrational degrees of freedom, that total energy = n_(1)[(kT)/2] + n_(2) [(kT)/2] + n_(3) [(kT)/2] xx 2 Where 'n' is atomicity of gas. The rotational kinetic energy of H20 molecule is equal to by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STATES OF MATTER BOOK - AAKASH SERIESCHAPTER - STATES OF MATTER EXERCISE - PRACTICE SHEET (EXERCISE-III) (KINETIC MOLECULAR THEORY, MOLECULAR VELOCITY, MEAN FREE PATH, COLLISION FREQUENCY) LEVEL-II (MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- STATES OF MATTER BOOK - AAKASH SERIESCHAPTER - STATES OF MATTER EXERCISE - PRACTICE SHEET (EXERCISE-III) (KINETIC MOLECULAR THEORY, MOLECULAR VELOCITY, MEAN FREE PATH, COLLISION FREQUENCY) LEVEL-II (INTEGER TYPE QUESTIONS)
1 Videos
- STATES OF MATTER BOOK - AAKASH SERIESCHAPTER - STATES OF MATTER EXERCISE - PRACTICE SHEET (EXERCISE-III) (KINETIC MOLECULAR THEORY, MOLECULAR VELOCITY, MEAN FREE PATH, COLLISION FREQUENCY) LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
2 Videos
- SOLUTIONS BOOK - AAKASH SERIESCHAPTER - SOLUTIONS EXERCISE - Objective Exercise -4
50 Videos
- STOICHIOMETRYBOOK - AAKASH SERIESCHAPTER - STOICHIOMETRYEXERCISE - PRACTICE SHEET (ADVANCED) (INTEGER TYPE QUESTION)
2 Videos
Similar Questions
Match the experimental facts (in List-I) with the explanation according to kinetic theory (in List-II):

View SolutionThe RMS velocity of nitrogen gas molecules is 'V cm/sec at a certain temperature. When the temperature is doubled, the molecules dissociated into individual atoms. Now the RMS velocity of nitrogen atoms is x V cm/sec. What is the value of 'x'?
View SolutionP and Q are ideal gases which do not react with each other. The mass of one mole of P is four times that of Q. At STP, which of the following are true?
View SolutionAssertion : Molarity of a solution decreases with an increase of temperature
Reason : As temperature increases volume of the solution increases.
View SolutionAmmonia is oxised by oxygen to give nitric oxide and water. The weight of water produced per gram of nitric oxide is 0.1×xg. What is value of d.
View SolutionIf e_(1)=E_(1)sin(omega_(1)t-k_(1)x+phi_(1)) and e_(2)=E_(2)sin(omega_(2)t-k_(2)x+phi_(2)) and e=e_(1)+e_(2) then show that E^(2)=E_(1)^(2)+E_(2)^(2)+2E_(1)E_(2)cos(delta_(2)-delta_(1)) where delta_(1)=omega_(1)t-k_(1)x+phi_(1) and delta_(2)=omega_(2)t-k_(2)x+phi_(2)
View SolutionTwo reaction : X→ Products and Y→ Products have rate constants k1 and k2 at temperature T and activation energies E1 and E2, respectively. If k1>k2 and E1<E2 (assuming that the Arrhenius factor is same for both the Products), then
(I) On increaisng the temperature, increase in k2 will be greater than increaisng in k1.
(II) On increaisng the temperature, increase in k1 will be greater than increase in k2.
(III) At higher temperature, k1 will be closer to k2.
(IV) At lower temperature, k1<k2
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
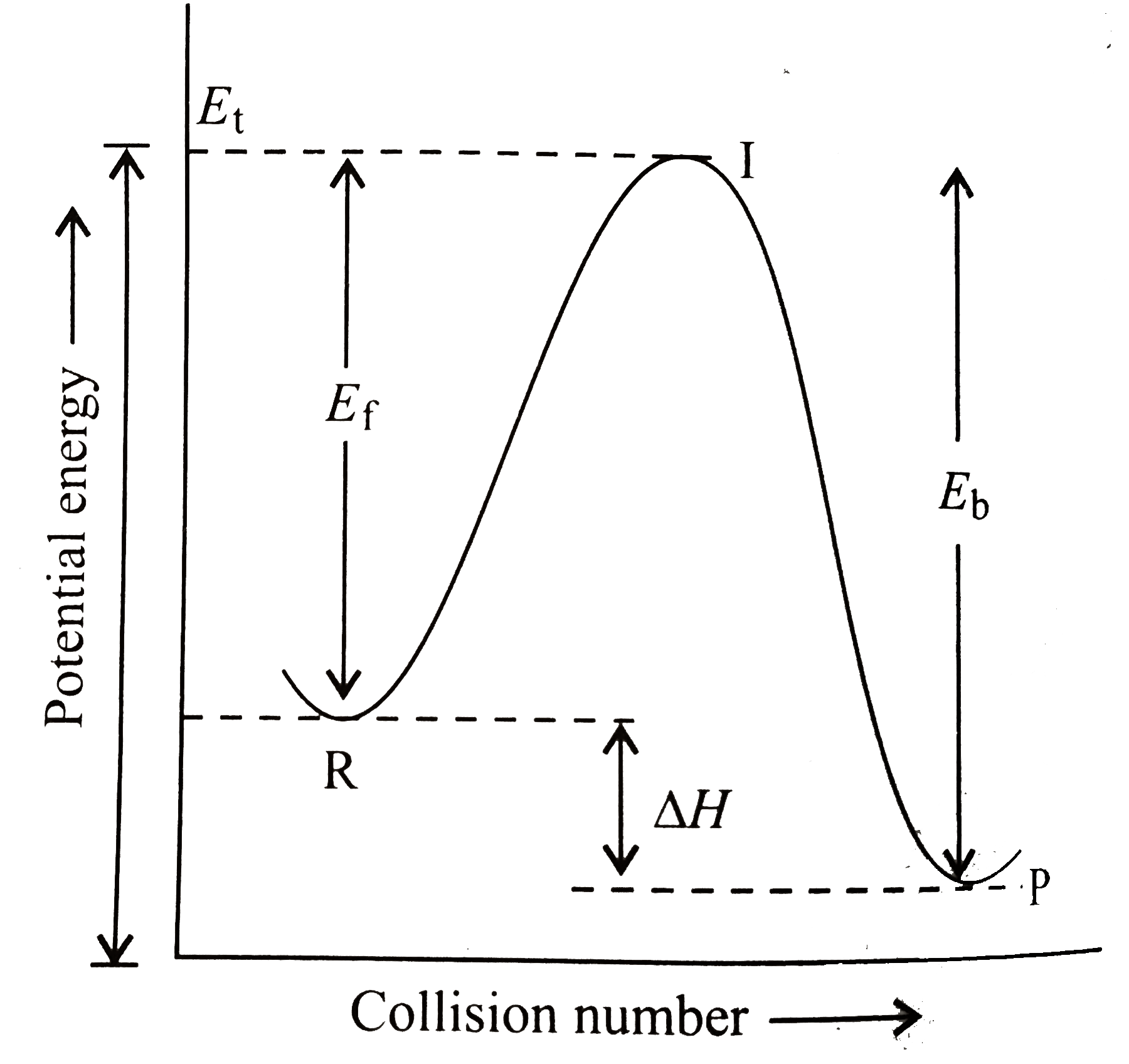
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
For two reactions, activation energies are Ea1 and Ea2, rate constant are k1 and k2 at the same temperature. If k1>k2, then
View SolutionA reaction takes place in theee steps: the rate constant are k_(1), k_(2), and k_(3) . The overall rate constant k=(k_(1)k_(3))/(k_(2)) . If E_(1), E_(2) , and E_(3) (energy of activation) are 60, 30 and 10kJ , respectively, the overall energy of activation is
View SolutionA reaction takes place in three steps. The rate constant are k1,k2 and k3. The overall rate constant k=k1k3k2. If E1,E2 and E3 (energy of activation) are 60, 30 and 10 kJ, respectively, the overall energy. Of activation is
View SolutionA reactant (A) froms two products, Aoverset(k_(1))toB , Activation Energy E_(a_(1)) Aoverset(k_(2))toB , Activation Energy E_(a_(2)) If E_(a_(1))=2E_(a_(2)) , then k_(1) and k_(2) are related as:
View SolutionA reactant (A) forms two products : A overset(k_(1))to B , Activation Energy E_(a_(1)) A overset(k_(2))to C , Activation Energy E_(a_(2)) If E_(a_(2))=2E_(a_(1)) , then k_(1) and k_(2) are related as
View Solution2A rarr B+C The mechanism of the above reaction given as 2A overset(K_(1))underset(K_(2))hArrX+2B (fast) X+B overset(K_(3))rarrC (slow) E_(1) = Activation energy for K_(1) K_(2) = Activation energy for K_(2) E_(3) =Activation energy for K_(3) Calculate E_("reaction") (given : E_(1) =10 kJ, E_(3)=5 kJ, E_(2) =12 kJ)
View Solutionदो स्प्रिंगों के बल नियतांक K1 व K2 है। उनमे समान खिंचाव x उत्पन्न किया जाता है । इनकी प्रत्यास्थ ऊर्जा E1 व E2 है तो E1 व E2 का अनुपात होगा ।
View SolutionA reactant (A) forms two products :
Ak1−−→B activation energy Ea1
Ak2−−→C activation energy Ea2
If Ea2=2Ea1, then k1 and k2 will be related as
View Solution
