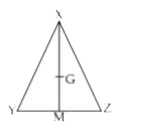
If the centroid of ΔMNP is G and MG = 5cm, then the median ¯¯¯¯¯¯¯MD in cm is
7.5
7
6.5
6
The correct Answer is:A
To find the length of the median ¯MD in triangle ΔMNP given that the centroid G divides the median ¯MD in the ratio 2:1 and MG=5 cm, we can follow these steps:
1. Understand the properties of the centroid: The centroid G of a triangle divides each median into two segments, where the segment connecting the vertex to the centroid is twice as long as the segment connecting the centroid to the midpoint of the opposite side. This means that if MG is the segment from vertex M to centroid G and GD is the segment from centroid G to midpoint D of side NP, then:
MGGD=21
2. Set up the relationship: Let MG=5 cm. According to the ratio 2:1:
MG=2×GD
Therefore, we can express GD in terms of MG:
GD=MG2=52 cm=2.5 cm
3. Calculate the total length of the median ¯MD: The total length of the median ¯MD is the sum of MG and GD:
MD=MG+GD=5 cm+2.5 cm=7.5 cm
4. Conclusion: Thus, the length of the median ¯MD is:
¯MD=7.5 cm
Final Answer:
The median ¯MD is 7.5 cm.
---
MGGD=21
MG=2×GD
Therefore, we can express GD in terms of MG:
GD=MG2=52 cm=2.5 cm
MD=MG+GD=5 cm+2.5 cm=7.5 cm
¯MD=7.5 cm
The median ¯MD is 7.5 cm.
Similar Questions
Knowledge Check
If the centroid of triangle ABC is G and BG = 9 cm, then what will be the length (in cm) of median BE?
A12B14C15D13.5If the centroid of triangle ABC is G and BG = 9 cm, then what will be the length (in cm) of median BE?
A12B14C15D13.5If G is the centroid of Δ ABC, then ¯¯¯¯¯¯CA+¯¯¯¯¯¯CB =
A3 ¯¯¯¯¯¯GCB3 ¯¯¯¯¯¯CGC3 ¯¯¯¯¯¯ABD3 ¯¯¯¯¯¯GA
In triangle XYZ, G is the centroid. If XY = 11 cm, YZ = 14 cm and XZ = 7 cm, then what is the value (in cm) of GM?
View SolutionIf G is centre of ΔABC and median AD = 12 cm. Find AG
View SolutionIf O is the centroid and AD, BE and CF are the three medians of ΔABC with an area of 96cm2 then the area of ΔBOD in cm2 is
View SolutionTwo medians AD and BE of ΔABC intersect at G at right angles . If AD=9cmandBE=6cm, them the length of BD (in cm) is
View SolutionIn ΔABC, AB = 7 cm, BC = 24 cm and AC = 25 cm. If G is the centroid of the triangle, then what is the length (in cm) of BG?
View Solution