Doubtnut Promotions Sticky

The equation of the circumcircle of the triangle formed by the lines whose combined equation is given by (x+y-4) (xy-2x-y+2)=0, is

A

x2+y2−5x−3y+8=0

B

x2+y2−3x−5y+8=0

C

x2+y2−3x−5y−8=0

D

none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

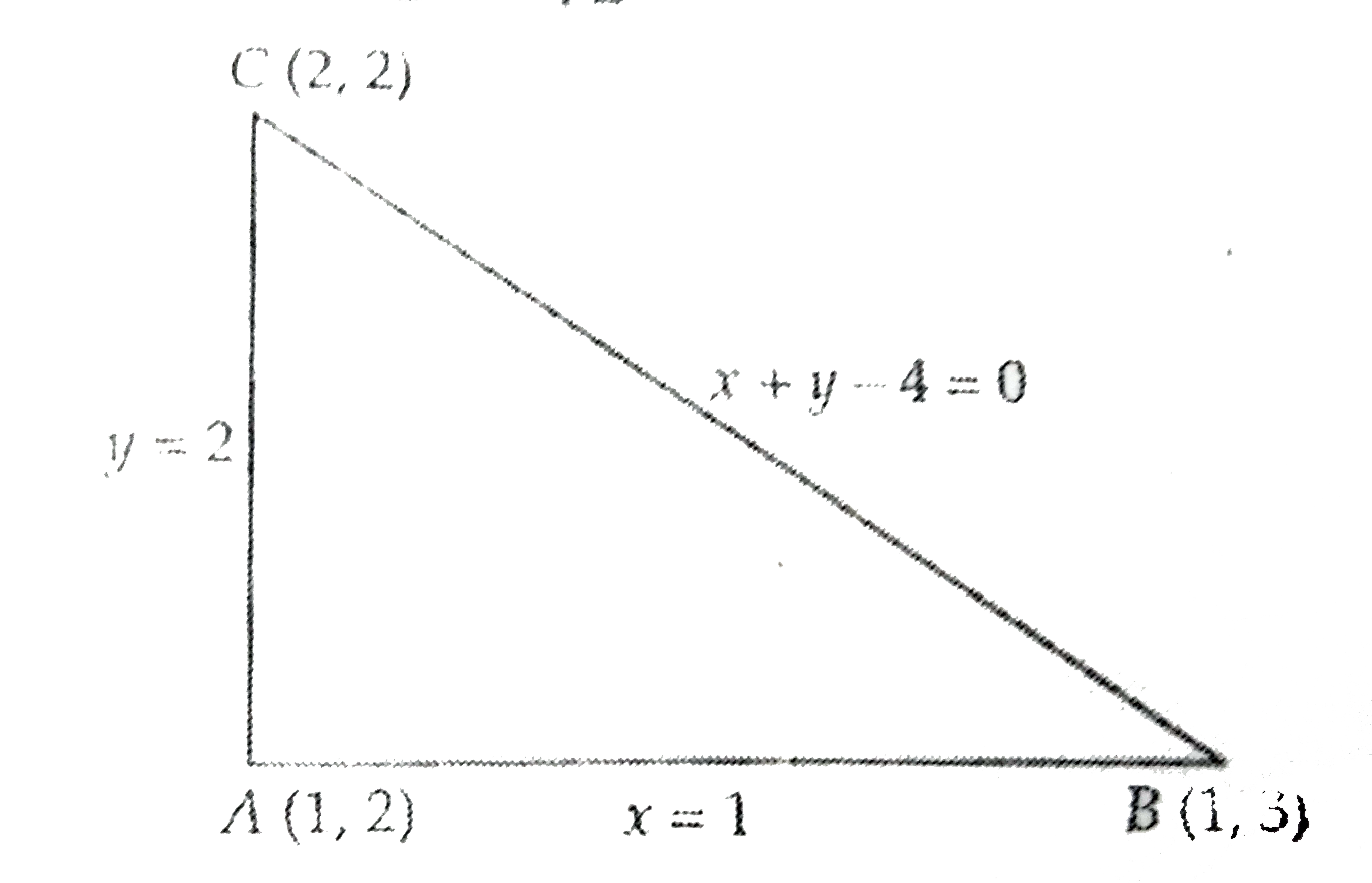
The combined equation of the sides of the triangle is
(x+y−4)(x−1)(y−2)=0⇒x+y−4=0,x=1,y=2
The equation of a second degree curve passing through the vertices of the triangle is
λ(x+y−4)(x−1)+μ(x−1)(y−2)+v(y−2)(x+y−4)=0 ...(i)
The equation will represent a circle, if
Coeff. of x2 = Coeff. of y2 and Coeff. of xy=0
⇒λ=vandλ+μ+v=0
⇒λ=vandμ=−2v
Substituting these values in (i), we obtain
(x+y−4)(x−1)−2(x−1)(y−2)(x+y−4)=0
⇒x2+y2−3x−5y+8=0
This is the equation of the required circumcircle .
ALITER–––––––––– The equations of the sides of the triangle are x+y-4=0, x=1 and y=2. Clearly, they form a right angled triangle. Therefore, circumcentre is the mid-point of hypotenuse and circumradius is half of the length of the hypotenuse. The coordinates of the circumcentre is (3/2, 5/2) and circumradius =√22=1√2
ocr_image
So, the equation of the circumcircle is
(x−32)2+(y−52)2=(1√2)2⇒x2+y2−3x−5y+8=0.

|
Updated on:21/07/2023
Class 12MATHSCIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The equation of the circumcircle of the triangle formed by the lines x=0, y=0, 2x+3y=5, is

    A6(x2+y2)+5(3x−2y)=0
    Bx2+y2+2x−3y+5=0
    Cx2+y2+2x−3y−5=0
    D6(x2+y2)−5(3x+2y)=0
  • Question 2 - Select One

    Orthocentre of the triangle formed by the lines whose combined equation is (y2−6xy−x2)(4x−y+7)=0 is

    A(1,2)
    B(2,3)
    C(0,1)
    Dnone of these
  • Question 3 - Select One

    The equation of circumcircle of the triangle formed by the lines x = 0, y = 0, 2x + 3y = 5 is :

    A6(x2+y2)+5(3x+2y)=0
    Bx2+y2−2x−3y+5=0
    Cx2+y2+2x−3y5=0
    D6(x2+y2)−5(3x+2y)=0