The circle which can be drawn to pass through (1, 0) and (3, 0) and to touch the y-axis intersect at angle $θ .$ Then $cos θ$ is equal to $\frac{1}{2}$ (b) $- \frac{1}{2}$ (c) $\frac{1}{4}$ (d) $- \frac{1}{4}$

A

$1 / 2$

B

$- 1 / 2$

C

$1 / 4$

D

$- 1 / 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

We have, $C_{1} A = C_{2} A = O D = 2$

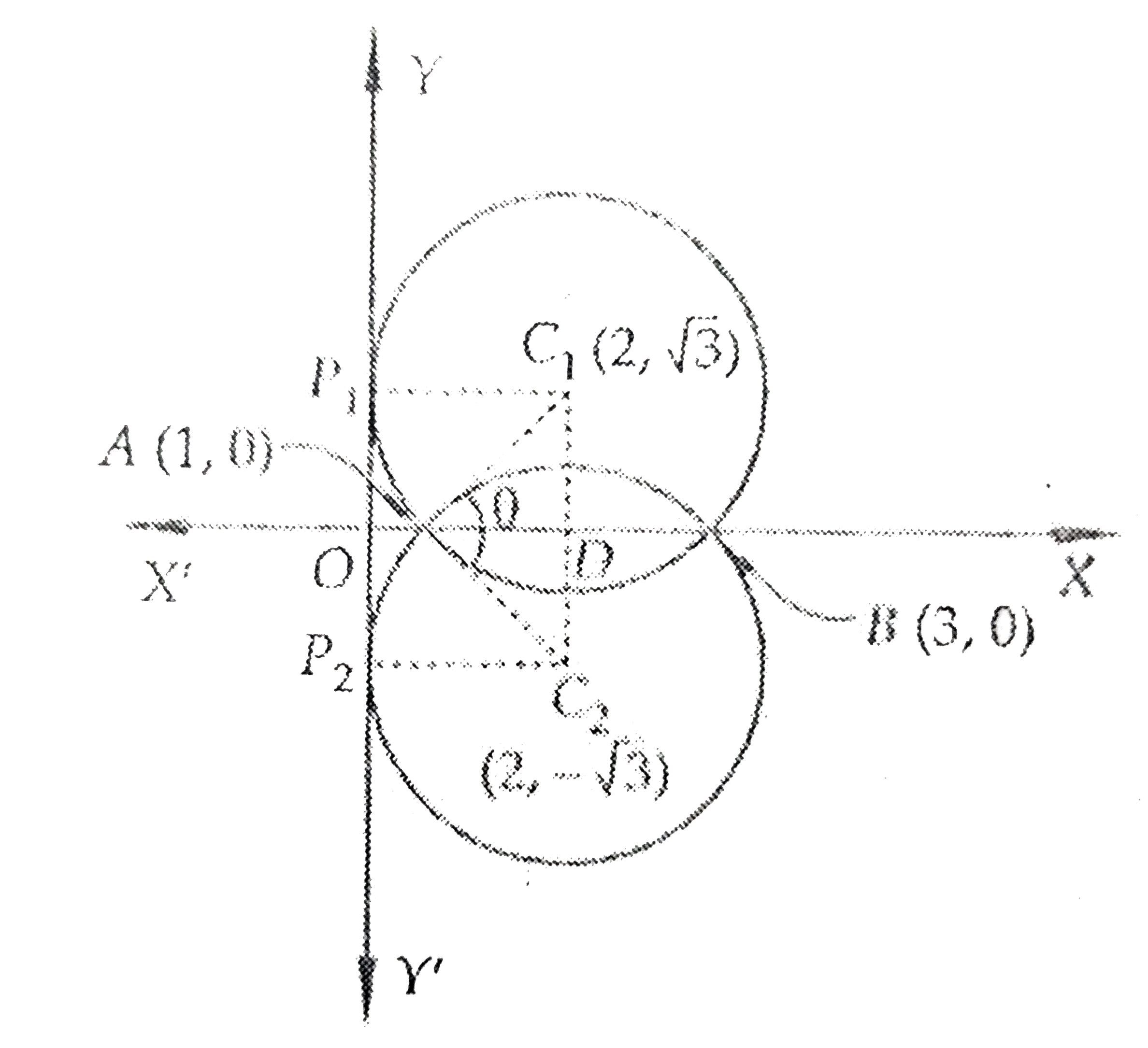
In $Δ O P_{1} C_{1}$ , we have
$O C_{1}^{2} = O P_{1}^{2} + C_{1} P_{1}^{2}$
$\Rightarrow 4 + 3 = O P_{1}^{2} + 2^{2} \Rightarrow O P_{1} = \sqrt{3}$
Thus, the coordinates of $C_{1}$ and $C_{2}$ are $(2, \sqrt{3})$ and $(2, - \sqrt{3})$
Thus, the coordinates of $C_{1} and C_{2}$ are $(2, \sqrt{3}) and (2, - \sqrt{3})$ respectively.

$cos θ = \frac{A C_{1}^{2} + A C_{2}^{2} - C_{1} C_{2}}{2 A C_{1} . A C_{2}} = \frac{4 + 4 - 12}{2 \times 2 \times 2} = - \frac{1}{2}$
$\Rightarrow θ = \frac{2 π}{3}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The circles which can be drawn to pass through (3,0) and (5,0) and to touch the y-axis intersect at an angle $θ$ , then $cos θ$ is equal to
A $7 / 8$
B $1 / 2$
C0
Dnone of these
Question 2 - Select One or More
Equations of circles which pass through the points (1,-2) and (3,-4) and touch the x-axis is
A $x^{2} + y^{2} + 6 x + 2 y + 9 = 0$
B $x^{2} + y^{2} + 10 x + 20 y + 25 = 0$
C $x^{2} + y^{2} - 6 x + 4 y + 9 = 0$
Dnone
Question 3 - Select One
The centre of the circle passing through (0, 0) and (1, 0) and touching the circle $x^{2} + y^{2} = 9$ , is
A(3/2, 1/2)
B(1/2, 3/2)
C(1/2, 1/2)
D $(1 / 2, \pm \sqrt{2})$

OBJECTIVE RD SHARMA-CIRCLES-Section I - Solved Mcqs

Home
Ask Doubt
Profile