From a point A(1, 1) on the circle two equal chords AB and AC of length 2 units are drawn. The equation of chord BC, is
4x+3y-12=0
x+y=4
3x+4y=4
x+y=6
The correct Answer is:B
It is evident from the figure that the chord BC is
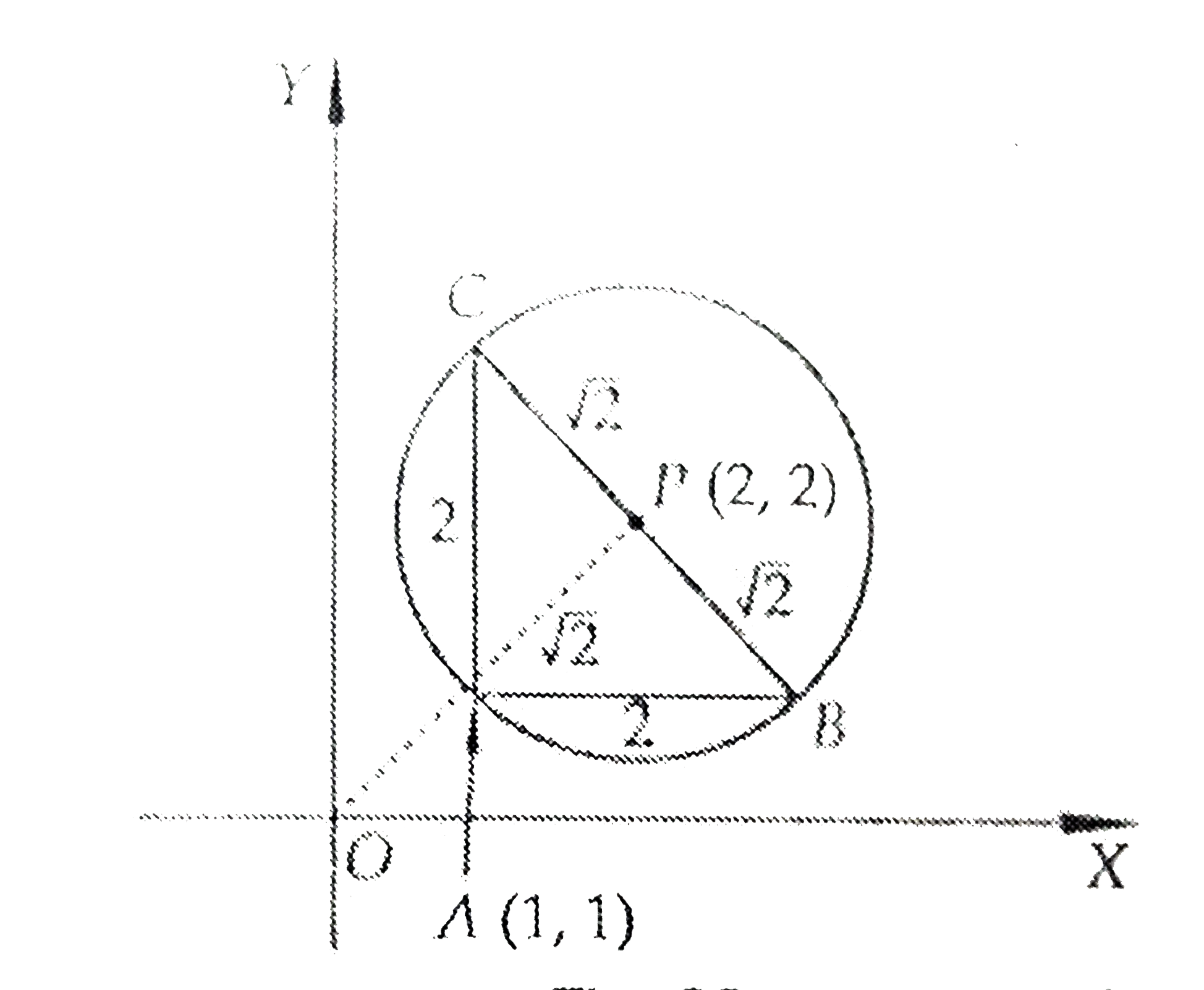
perpendicular to AP and passes through the centre P(2,2). So, its equation is x+y=4.
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type
12 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
Knowledge Check
From a point P(3, 3) on the circle x2+y2=18 , two chords PQ and PR each of 2 units length are drawn on this circle. The value of cos (∠QPR) is equal to
A13√2B−89C√23D−49Tangents drawn from the point (4,4) to the circle
x2+y2−2x−2y−7=0 meets the circle at A andB then the length of chord AB is equal toA2√3B3√2C4√3D2√6If from the origin a chord is drawn to the circle x2+y2−2x=0, then the locus of the mid point of the chord has equation
Ax2+y2+x+y=0Bx2+y2+2x+y=0Cx2+y2−x=0Dx2+y2−2x+y=0
From the point A(0, 3) on the circle x2+4x+(y−3)2=0, a chord AB is drawn and extended from point B to a point M such that AM = 2AB. The perimeter of the locus of M is pπ units. Then, the value of p is
View SolutionThe locus of mid-points of the chords of the circle x2−2x+y2−2y+1=0 which are of unit length is :
View SolutionFor the circle x2+y2−2x−6y+1=0 the chord of minimum length and passing through (1, 2) is of length-
View SolutionFrom (3,4) chords are drawn to the circle x2+y2−4x=0. The locus of the mid points of the chords iS :
View SolutionTwo tangents are drawn from the point P(−1,1) to the circle x2+y2−2x−6y+6=0. If these tangen tstouch the circle at points A and B, and if D is a point on the circle such that length of the segments AB and AD are equal, then the area of the triangle ABD is equal to
View Solution
