A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3 sqrt3/2, 3/2). Further, it is given that the origin and the centre of C are on the same side of the line PQ. (1)The equation of circle C is (2)Points E and F are given by (3)Equation of the sides QR, RP are
(x−2√3)2+(y−1)2=1
(x−2√3)2+(y+12)2=1
(x−√3)2+(y+1)2=1
(x−√3)2+(y−1)2=1
The correct Answer is:D
Let A(h,k) be the centre of the circle. Then, AD⊥PQ and AD=1
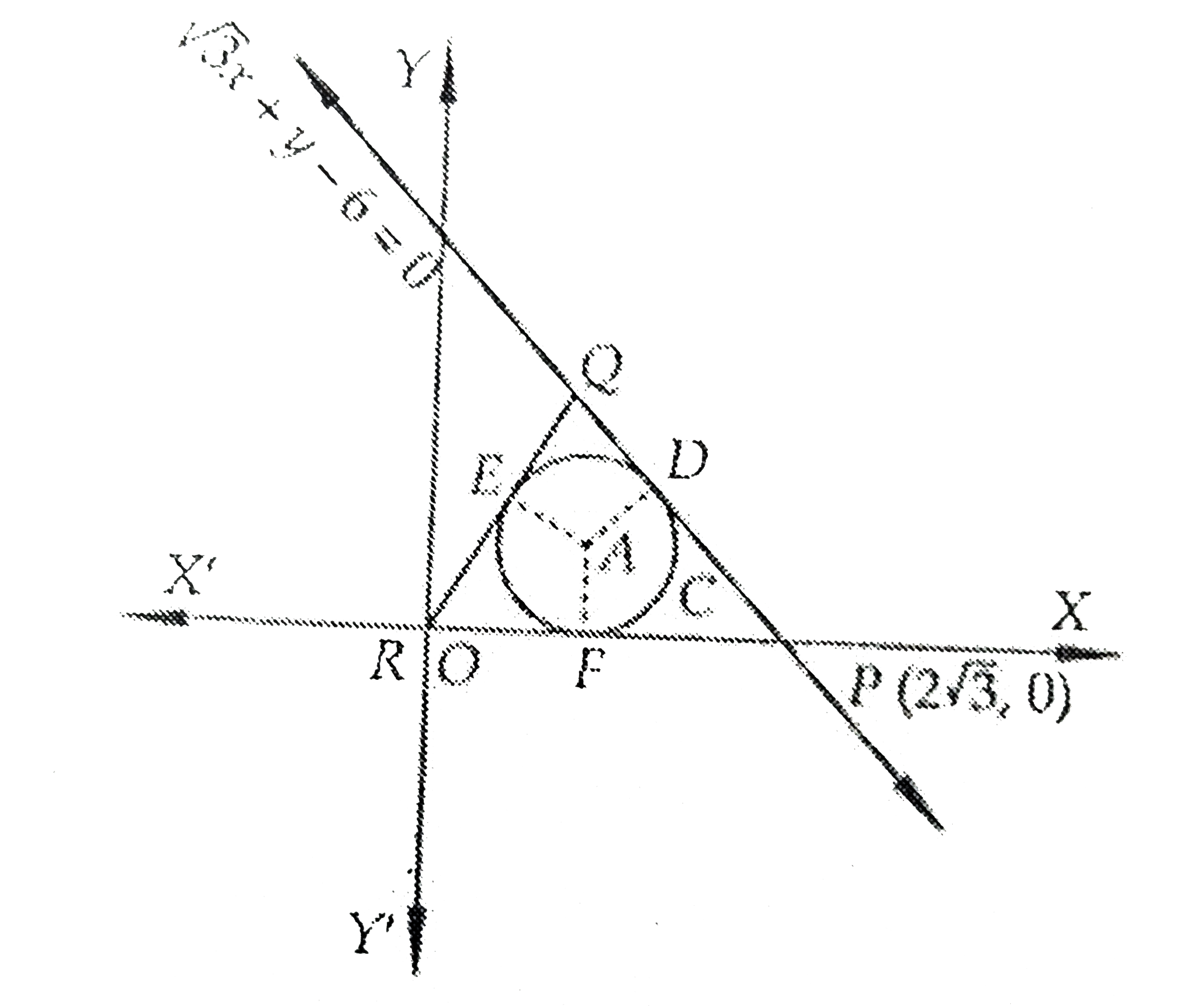
⇒2k−32h−3√3×(−√3)=−1and∣∣∣√3h+k−6√3+1∣∣∣=1
⇒2√3k−3√3=2h−3√3and∣∣√3h+k−6∣∣=2
⇒2h−2√3k=0and√3h+k−6=2or√3h+k−6=−2
⇒h=√3kand√3h+k−6=−2
[∴( Origin and (h, k) lie on the same side of √3x+y−6=0),(.∴√3h+k−6<0)]
⇒h=√3kand√3h+k=4
⇒h=√3,k=1
Hence, the equation of circle C is (x−√3)2+(y−1)2=1
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type
12 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
A circle of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QH and RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3√32,32). Further, it is given that the origin and the centre of C are on the same side of the line PQ.
The equation of circle C is
View SolutionA circle of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QH and RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3√32,32). Further, it is given that the origin and the centre of C are on the same side of the line PQ.
Equations of the sides QR, RP are
View Solution
Knowledge Check
A circle of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QH and RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3√32,32). Further, it is given that the origin and the centre of C are on the same side of the line PQ.
Points E andF are given byA(√32,32),(√3,0)B(√32,12),(√3,0)C(√32,32),(√32,12)D(32,√32),(√32,12)In a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of thesePQRS is a quadrilateral having 3 4 5 6 points on PQ , QR, RS and SP respectively. The number of triangles with vertices on different sides is
A220B270C282Dnone of these
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32). Equation of the sides QR,RP are : (A) y=2√3x+1,y=2√3x−1 (B) y=1√3x,y=0 (C) y=√32x+1,y=√32x−1 (D) y=√3x,y=0
View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32). Point E and F are given by : (A) (√32,32),(√3,0) (B) (√32,32),(√32,12) (C) (32,√32),(√32,12)
View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32) The equation of circle C is : (A) (x−2√3)2+(y−1)2=1 (B) (x−2√3)2+(y+12)2=1 (C) (x−√3)2+(y+1)2=1 (D)(x−√3)2+(y−1)2=1
View SolutionNumber of equilateral triangle with y=√3(x−1)+2;y=−√3x as two of its sides is
View SolutionThe vertex P of an equilateral triangle △PQR is at (2,3) and the equation of the opposite side QR is given by x+y=2. Find the possible equations of the side PQ.
View Solution
