Let (x,y)be such that
sin−1(ax)+cos−1y+cos−1(bxy)=π2
If a=1 alnd b=2 then (x,y)lies on
A
x2+y2=1
B
(x2−1)(y2−1)=0
C
y=x
D
(4x2−1)(y2−1)=0
Video Solution
Text Solution
If a =1 b=2 then
sin−1(ax)+cos−1y+cos−1(byx)=π2
→sin−1x+cos−1y+cos−1(2xy)=π2
→xy+√1−x2√1−y2=2xy
→x2+y2=1
|
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Section II - Assertion Reason Type
11 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise
72 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Chapter Test
30 Videos
- INTEGRALSBOOK - OBJECTIVE RD SHARMACHAPTER - INTEGRALSEXERCISE - Illustration
1 Videos
- LIMITSBOOK - OBJECTIVE RD SHARMACHAPTER - LIMITSEXERCISE - Chapter Test
60 Videos
Similar Questions
Let (x,y) be such that sin−1(ax)+cos−1(bxy)=π2 If a=1andb=0, then (x,y)
View SolutionLet (x,y) be such that sin−1(ax)+cos−1(y)+cos−1(bxy)=π2 Match the statement in Column I with the properties in Column II and indicate your answer by darkening the appropriate bubbles in the 4×4 matrix.
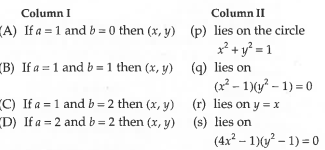
View Solution
Knowledge Check
If sin−1x+cos−1y+sin−1z=2π then 2x−z+y is :
A4B2C0D3If sin−1x+sin−1y=2π3andcos−1x−cos−1y=π3, then (x,y)=
A(0,1)B(1/2,1)C(1,1/2)D(√3/2,1)If sin−1x+sin−1y=2π3andcos−1x−cos−1y=π3, then (x,y)=
A(1,1)B(12,1)C(1,12)D(13,13)
If sin−1x+sin−1y=π3 and cos−1x−cos−1y=π6 , find the values of x and y .
View SolutionIf sin−1(x2−4x+5)+cos−1(y2−2y+2)=π2 then find the value of xandy.
View SolutionIf sin−1x+cos−1y=2π5,then cos−1x+sin−1y=
View SolutionIf sin−1x+sin−1y=2π3, then: cos−1x+cos−1y=
View SolutionIf sin−1x+sin−1y=π2andsin2x=cos2y, then
View Solution
