Question

Let $f:[0,4\pi ]\to [0,\pi ]$ be defined by $f\left(x\right)={\cos }^{-1}\left(\cos x\right).$ The number of points $x\in [0,4\pi ]$ 4satisfying the equation $f\left(x\right)=\frac{10-x}{10}$ is

Options

A. 2
B. 3
C. 4
D. 5

Explanation

Clearly the number of solution of `f(x) =(10x)/(10)` is same as the number of points of intersection of the curves `f(x)=cos(cos^(-1)x) and y =(10-x)/(10)` in he interval `[0,4pi]`

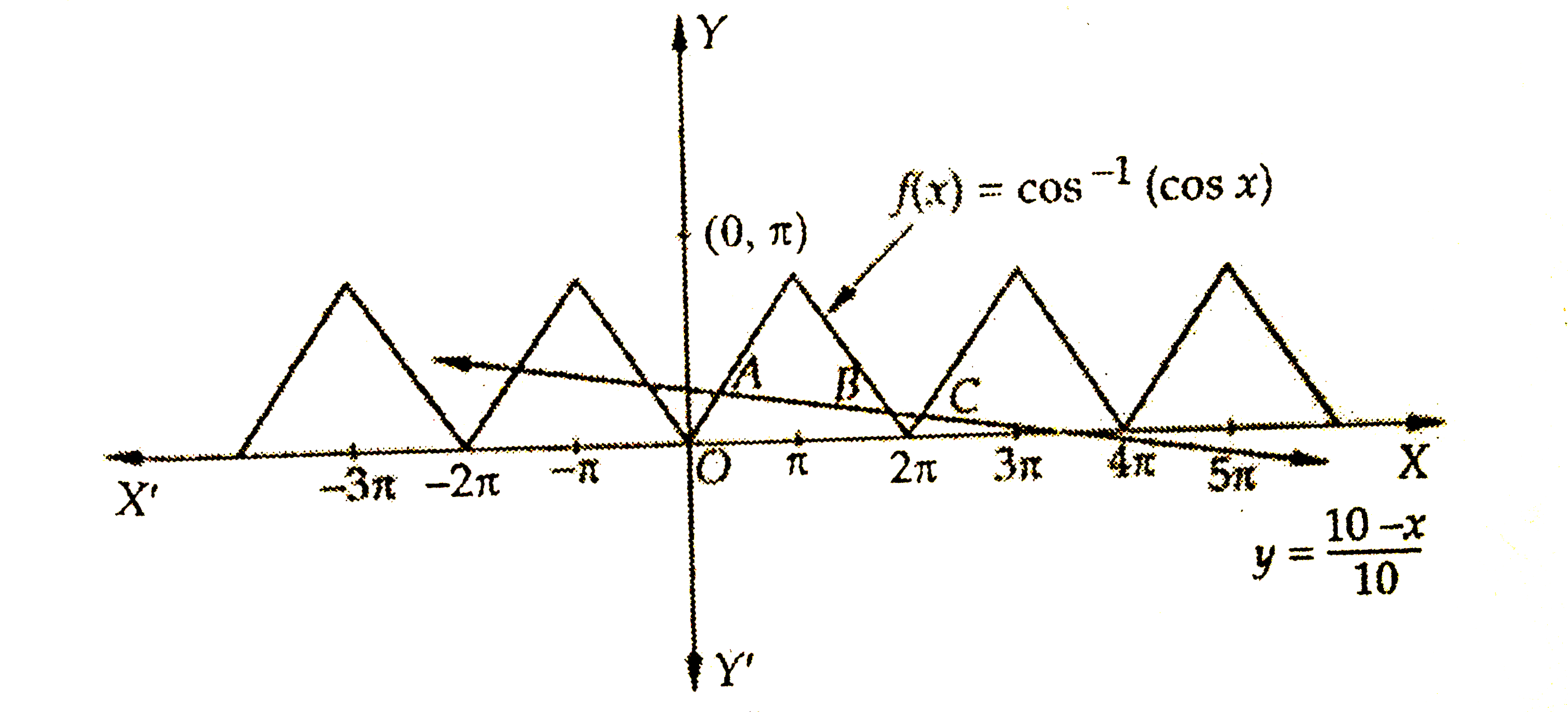
It is evident form that the two curves intersect at three points viz a,b,c so the given equation has three solution in the interval `[0,4pi]`