If A=[sinαcosα−cosαsinα] , verify that AT A=I2 .Solution in Gujrati
Step by step video & image solution for If A=[sinalphacosalpha-cosalphasinalpha] , verify that A^T\ A=I_2 . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MATRICESBOOK - NCERT GUJARATICHAPTER - MATRICESEXERCISE - EXERCISE 3.4
18 Videos
- MATRICESBOOK - NCERT GUJARATICHAPTER - MATRICESEXERCISE - Miscellaneous Exercise on Chapter 3
15 Videos
- MATRICESBOOK - NCERT GUJARATICHAPTER - MATRICESEXERCISE - EXERCISE 3.2
22 Videos
- LINEAR PROGRAMMINGBOOK - NCERT GUJARATICHAPTER - LINEAR PROGRAMMINGEXERCISE - MISCELLANEOUS EXERCISE
6 Videos
- PROBABILITYBOOK - NCERT GUJARATICHAPTER - PROBABILITYEXERCISE - MISCELLANEOUS EXERCISE ON CHAPTER 13
18 Videos
Similar Questions
Using elementary transformations, find the inverse of the matrix[1−123]
View SolutionLet A A=[0100] , show that (aI+bA)n=anI+nan−1bA, where I is the identity matrix of order 2 and n∈N.
View SolutionA=[2432],B=[13−25],C=[−2534]
find each of the following :
(i) A+B (ii) A-B
(iii) 3A-C (iv) AB
(V) BA
View SolutionA farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs. 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs. 200 pre bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element c. The minimum requirements of nutrients A,B and C are 18 units, and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag.
View SolutionA and B are two events such that P(A)≠0. Find P(B|A), if
(i) A is a subset of B (ii) A∩B=ϕ
View SolutionIf Aα=[cosαsinα−sinαcosα],thenAαAβ= (a)Aα+β (b) Aαβ (c) Aα−β (D) None of these
View SolutionProve that the product of the matrices [[cos^2alpha, cosalphasinalpha],[cosalphasinalpha,sin^2alpha]] and [[cos^2beta,cosbetasinbeta],[cosbetasinbeta,sin^beta]] is the null matrix when alpha and beta differ by an odd multiple of pi/ 2.
View SolutionIn the circuit shown switch S is closed at t=0. Let i1 and i2 be the current at any finite time t then the ratio i1i2
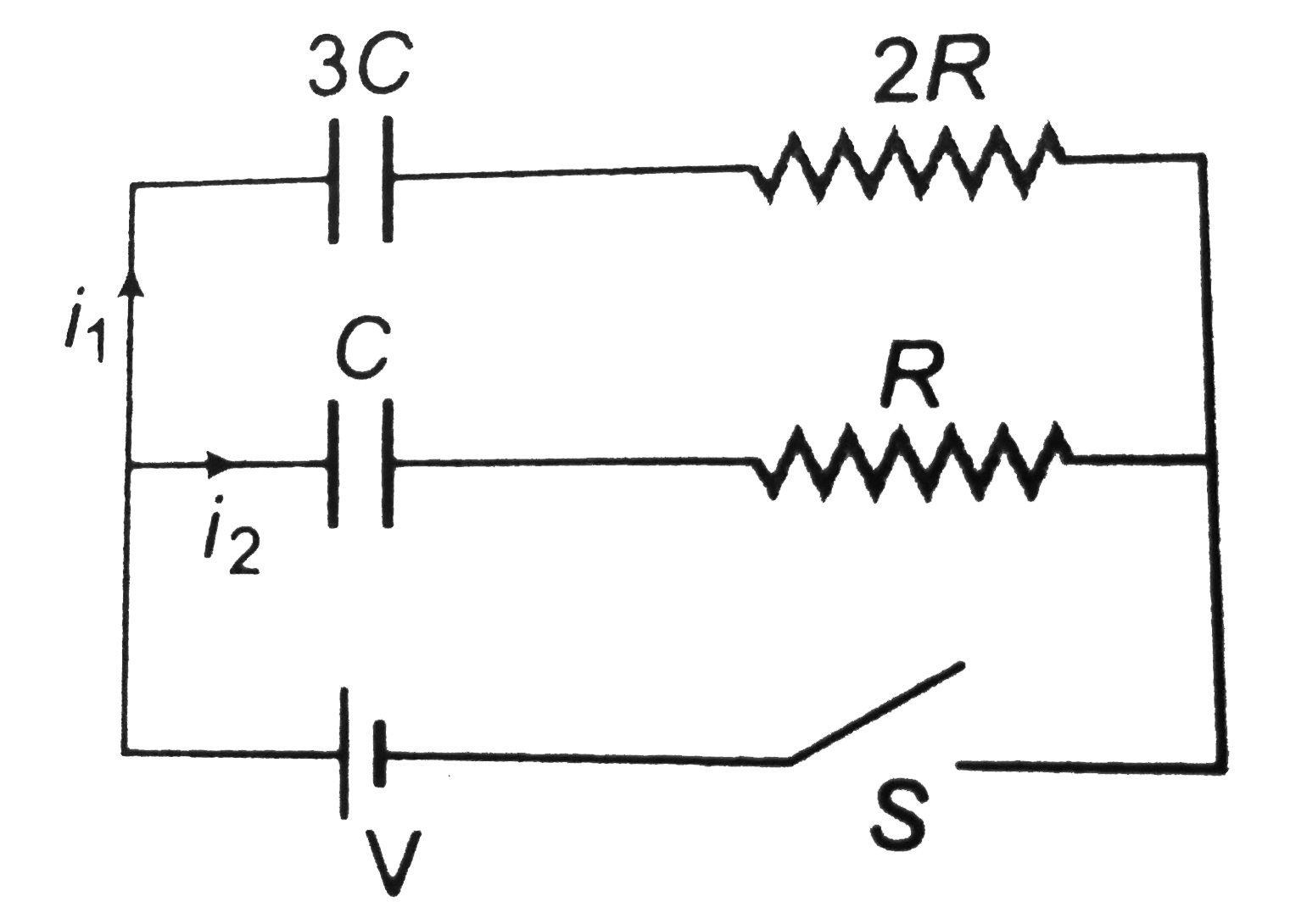
View SolutionIn the circuit shwon in fig. switch S is closed at time t = 0. Let I_1 and I_2 be the currents at any finite time t, then the ratio I_1// I_2
View SolutionIf A=[cosθ−sinθsinθcosθ],thenAT+A=I2, if
View SolutionA=[cos2αcosαsinαcosαsinαsin2α]
B=[cos2βcosβsinβcosβsinβsin2β]
are two matrices such that the product AB is the null matrix, then (α−β) is
View SolutionIf Aα=[cosαsinα−sinαcosα] , then prove that (Aα)n=[cosn αsinn α−sinn αcosn α] for every positive integer n .
View SolutionIf A=[cosαsinα−sinαcosα] , then verify that AT A=I2 .
View SolutionIf A=[sinαcosα−cosαsinα], verify that ATA=I2
View SolutionIf αandβ are not the multiple of π2and[cos2αcosαsinαcosαsinαsin2α]×[cos2βsinβcosβsinβcosβsin2β]=[0000]then α−β is ......
View SolutionIn the circuit shown switch S is closed at t=0 . Let i_1 and i_2 be the current at any finite time t then the ratio i_1/i_2
View Solution
