The velocity-time graph of a particle in one-dimensional motion is shown in Fig.

Which of the following formulae are correct for describing the motion of the particle over the time-interval t1 to t2 :
(a) x(t2)=x(t1)+υ(t1)(t2−t1)+(1/2)a(t2−t1)2
(b) υ(t2)=υ(t1)+a(t2−t1)
(c ) υaverage=(x(t2)−x(t1))/(t2−t1)
(d) aaverage=(υ(t2)−υ(t1))/(t2−t1)
(e ) x(t2)=x(t1)+υaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(f) x(t2)−x(t1)= area under the υ−t curve bounded by the t-axis and the dotted line shown.
(c ), (d), (f)
Topper's Solved these Questions
Similar Questions
The angle of elevation of a bird sitting on top of a tree as seen from the point at a distance of 20m from the base of the tree is 60∘. Then, the height of the tree is ……..m
12:25View SolutionState , for each of the following physical quantities , if it is a scalar or a vector : volume , mass , speed , acceleration , density , number of moles , velocity , angular frequency , displacement , angular velocity .
05:58View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
 03:15View Solution
03:15View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
05:36View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig.:

(a) Which of the following formulae are correct for describing the motion of the particle over the time-interval t1 to t2:
(a) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(b) v(t2)=v(t1)+a(t2−t1)
(c) vaverage=(x(t2)−x(t1))/(t2−t1)
(d) aaverage=(v(t2)−v(t1))/(t2−t1)
(e) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(f) x(t2)−x(t1) = area under the v−t curve bounded by the t-axis and the dotted line shown.03:27View SolutionFor any arbitrary motion in space, which of the following relations are true?
(a) vaverage=(1/2)(v(t1)+v(t2))
(b) vaverage=[r(t2)−r(t1]/(t2−t1)
(c) v(t)=v(0)+at
(d) aaverage=[v(t2)−v(t1)]/(t2−t1)
The average stands for average of the quantity over time interval t1 to t203:03View Solutionएकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र 3.29 में दिखाया गया है :

नीचे दिए सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-सा सूत्र सही है :
(i) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(ii) v(t2)=v(t1)+a(t2−t1)
(iii) vaverage=[x(t2)−x(t1)]/(t2−t1)
(iv) aaverage=[v(t2)−v(t1)]/(t2−t1)
(v) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(vi) x(t2)−x(t1)=t-अक्ष तथा दिखाई गई बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल |05:03View Solutionएक विमीय गति में किसी का वेग - समय ग्राफ चित्र 3.62 में दिखाया गया है नीचे दिए सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही है
vaverage=[x(t2)−x(t1)]/(t2−t1)
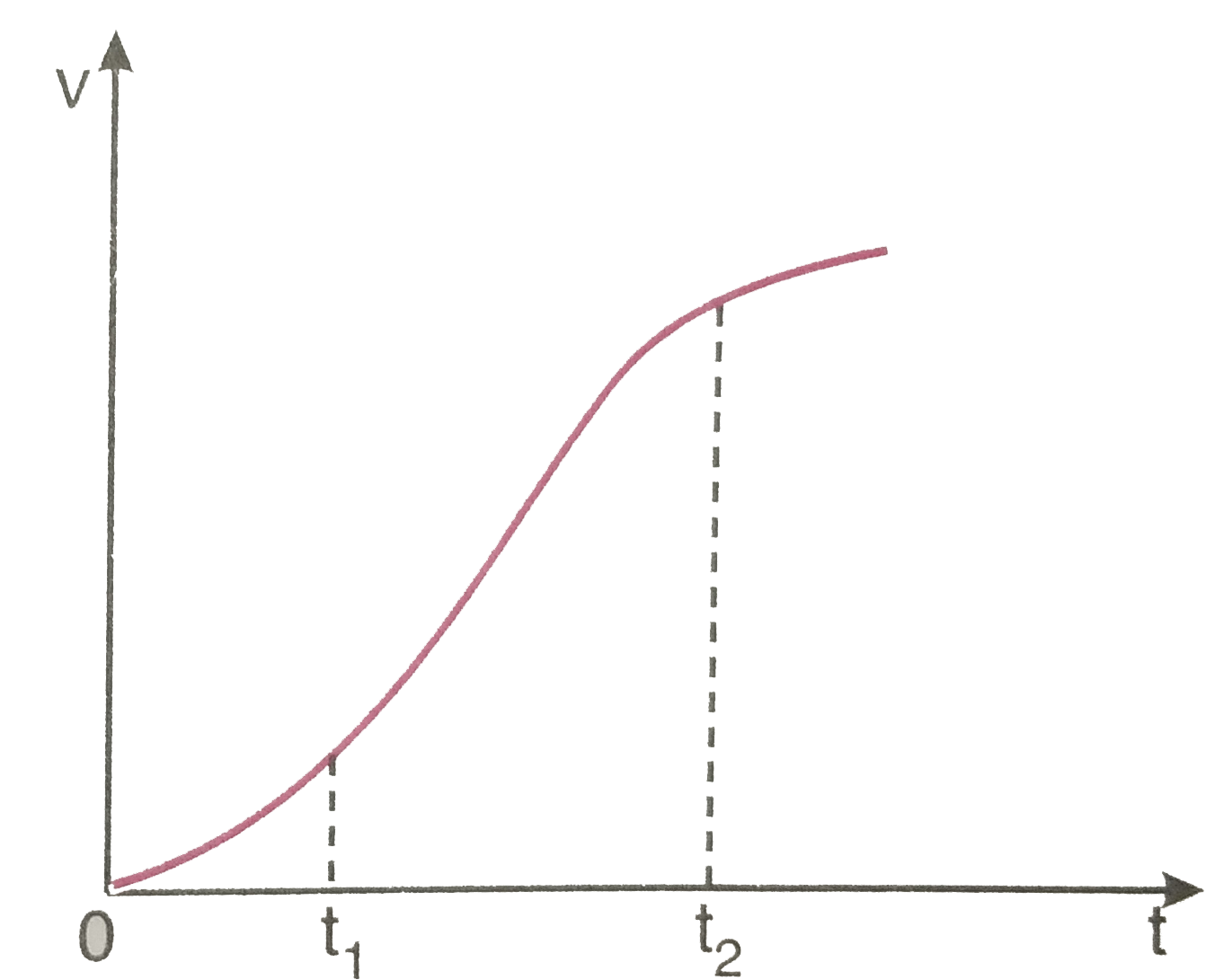 05:03View Solution
05:03View Solutionएक विमीय गति में किसी का वेग - समय ग्राफ चित्र 3.62 में दिखाया गया है नीचे दिए सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही है
aaverage=[v(t2)−v(t1)]/(t2−t1)
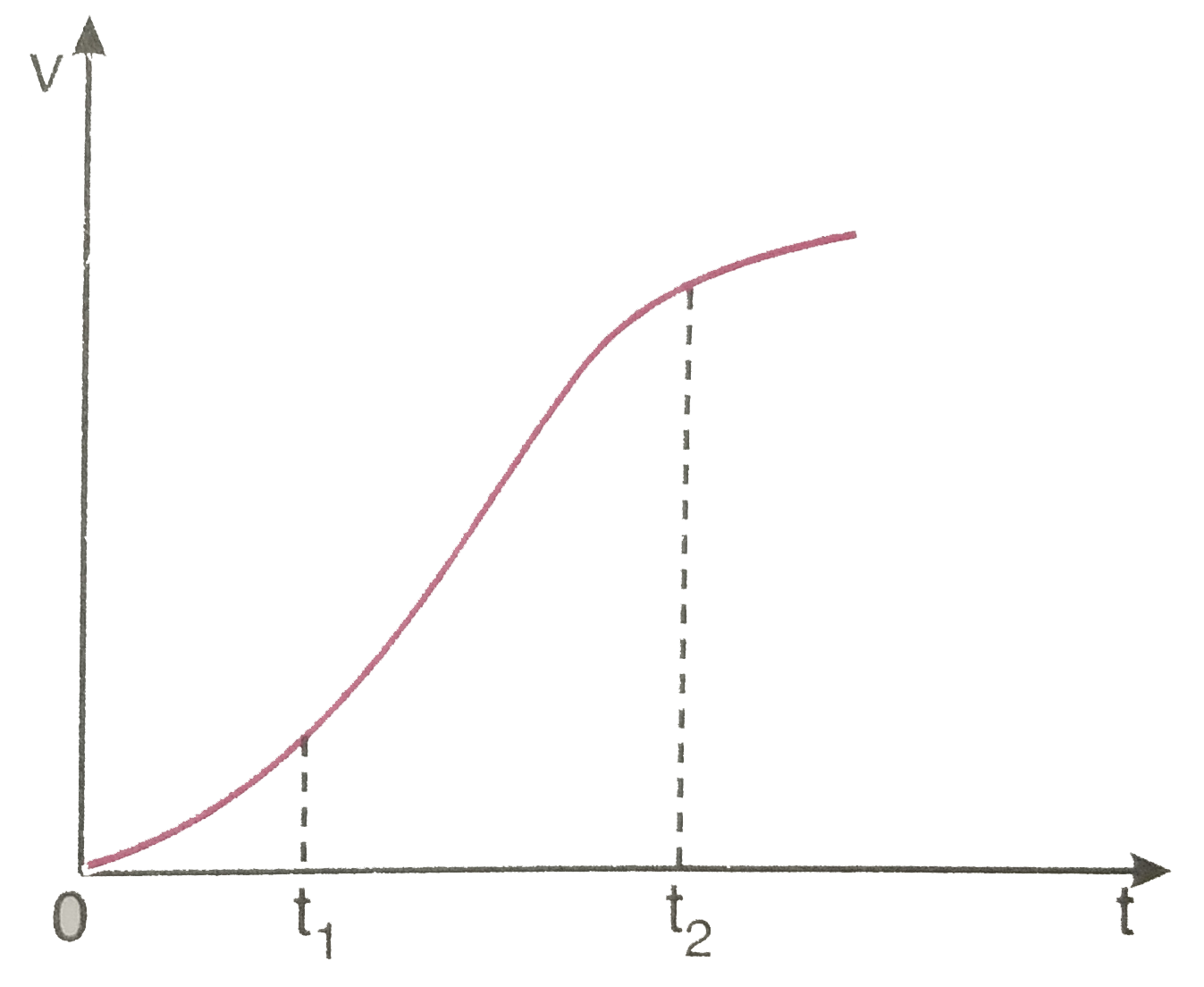 03:32View Solution
03:32View Solutionएकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र में दिखाया गया है -
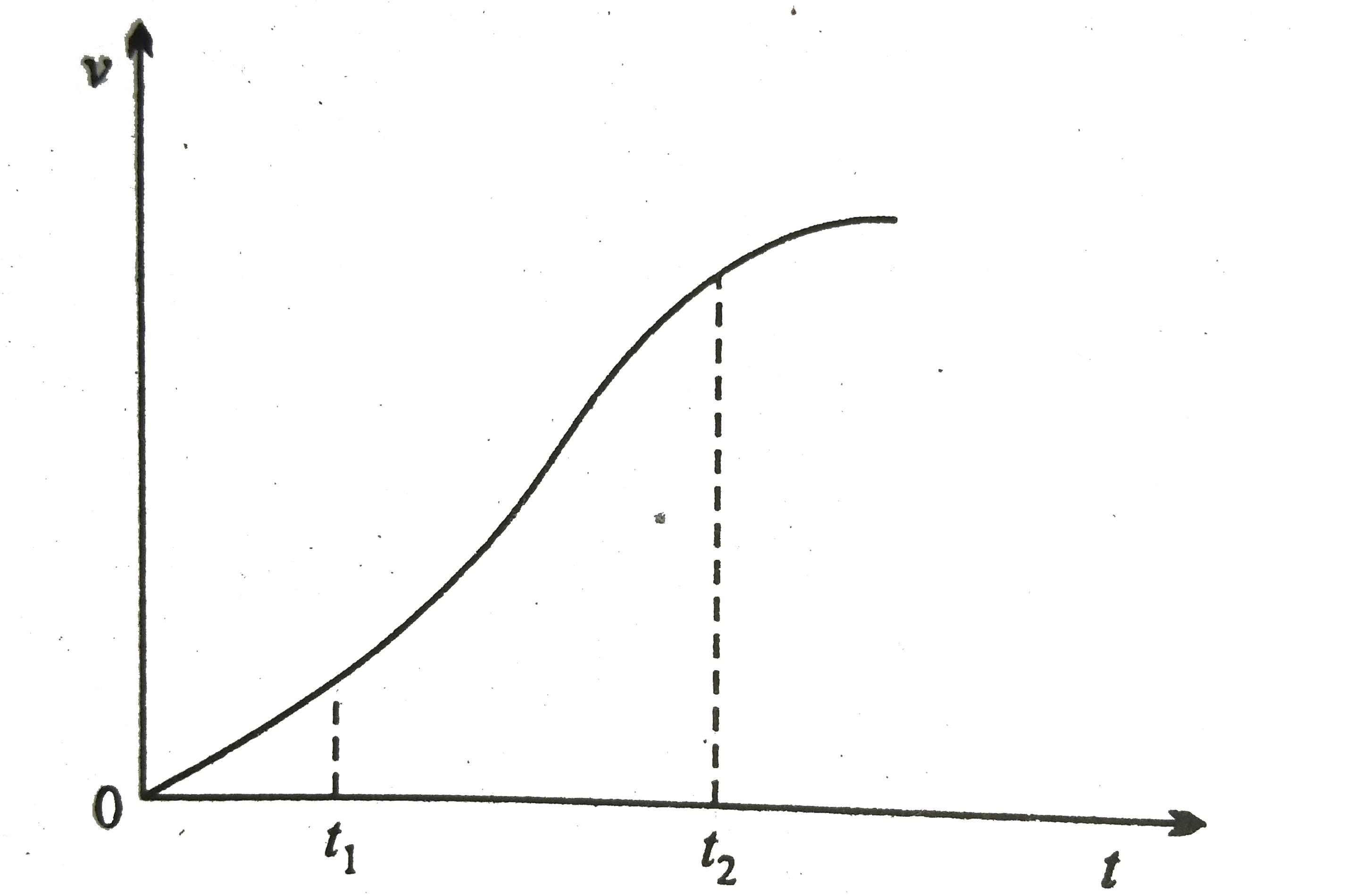
नीचे दिये सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही हैं -
(i) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(ii) v(t2)=v(t1)+a(t2−t1)
(iii) vaverage=[x(t2)−x(t1)]/(t2−t1)
(iv) vaverage=[v(t2)−v(t1)]/(t2−t1)
(v) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(vi) x(t2)−x(t1)=t− अक्ष तथा दिखाई गाड़ी बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल ।View Solutionएकविमीय गति में किसी कण का वेग - समय ग्राफ चित्र में दिखाया गया है-
दिए सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन - से सूत्र सही हैं
(i) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(i8i) v(t2)=v(t1)+a(t2−t1)
(iii) vaverage=[x(t2)−x(t1)]/(t2−t1)
(iv) aaverage=[v(t2)−v(t1)]/(t2−t1)
(v) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
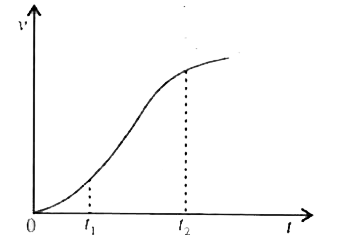
(vi) x(t2)−x(t1)=t− अक्ष तथा दिखाई गई बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल |03:25View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig.
Which of the following formulae are correct for describing the motion of the particle over the time-interval t1 to t2 :
(a) x(t2)=x(t1)+υ(t1)(t2−t1)+(1/2)a(t2−t1)2
(b) υ(t2)=υ(t1)+a(t2−t1)
(c ) υaverage=(x(t2)−x(t1))/(t2−t1)
(d) aaverage=(υ(t2)−υ(t1))/(t2−t1)
(e ) x(t2)=x(t1)+υaverage(t2−t1)+(1/2)aaverage(t2−t1)2
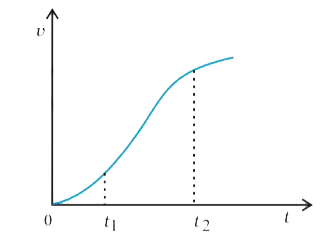
(f) x(t2)−x(t1)= area under the υ−t curve bounded by the t-axis and the dotted line shown.03:29View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig.
Which of the following formulae are correct for describing the motion of the particle over the time-interval t1 to t2 :
(a) x(t2)=x(t1)+υ(t1)(t2−t1)+(1/2)a(t2−t1)2
(b) υ(t2)=υ(t1)+a(t2−t1)
(c ) υaverage=(x(t2)−x(t1))/(t2−t1)
(d) aaverage=(υ(t2)−υ(t1))/(t2−t1)
(e ) x(t2)=x(t1)+υaverage(t2−t1)+(1/2)aaverage(t2−t1)2
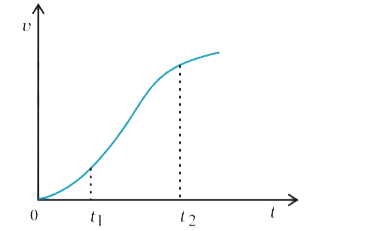
(f) x(t2)−x(t1)= area under the υ−t curve bounded by the t-axis and the dotted line shown.View SolutionProve that the point of intersection of the tangents at t1andt2 on the parabola y2=4ax is (at1t2,a(t1+t2))
02:40View SolutionFollowing are four different relation about displacement,velocity and acceleration for the motion of a particle in general.Choose the incorrect one (S). a) V_(av)=(1)/(2)[v(t_(1))+v(t_(2))] b) V_(av)=(r(t_(2))-r(t_(2)))/(t_(2)-t_(1)) c)r= (1)/(2)(v(t_(2))-v(t_(1))(t_(2)-t_(1)) d) a_(av)=(v(t_(2))-v(t_(1)))/(t_(2)-t_(1))
06:44View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal toView Solution

