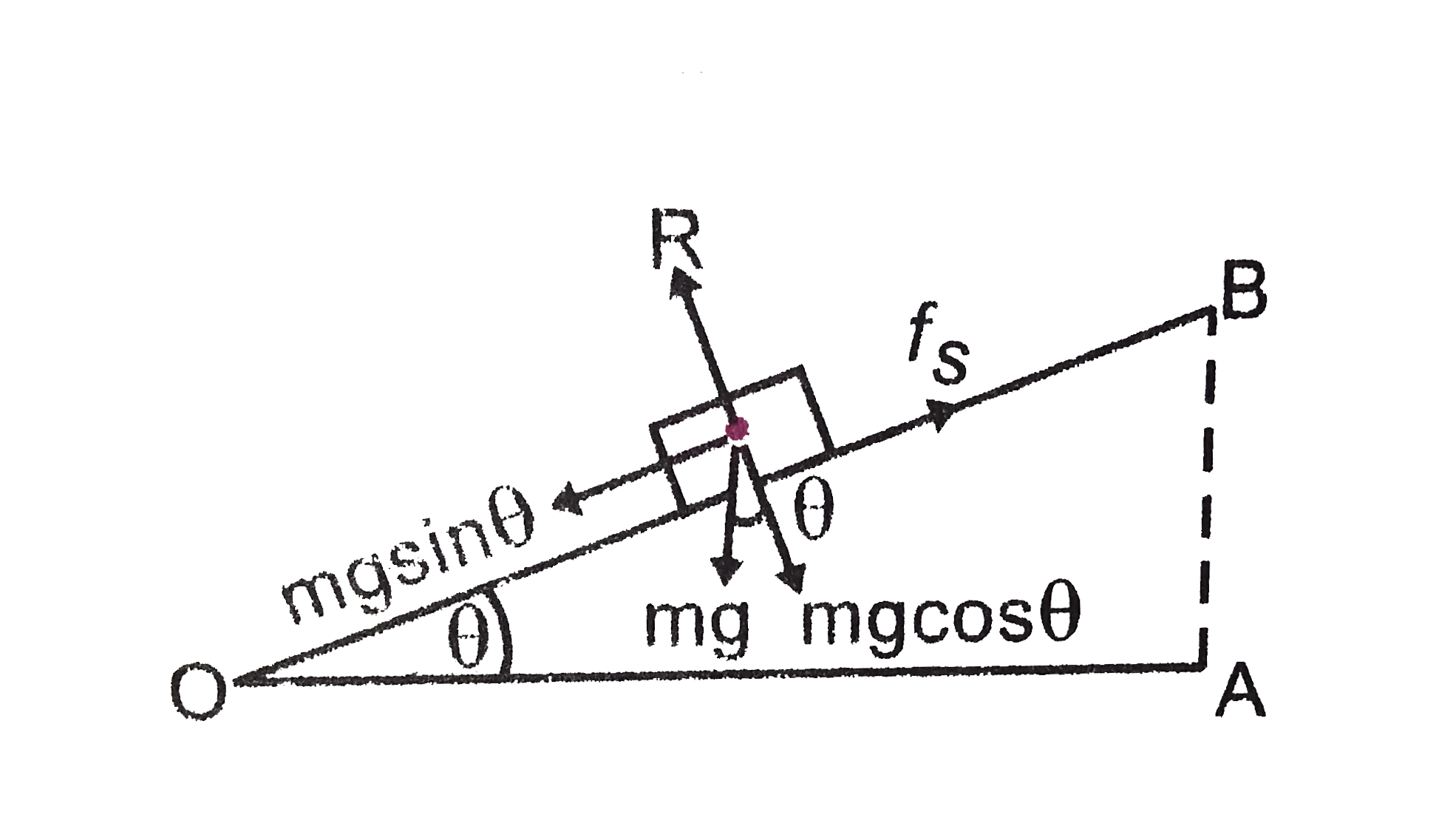
See Fig. A mass of 4 kg rests on a horizontal plane. The plane is gradually inclined until at an angle θ=15∘ with the horizontal, the mass just begins to slide. What is the coefficient of static friction between the block and the surface ?

The forces acting on a block of mass m at rest on an inclined plane are (i) the weight mg acting vertically downwards (ii) the normal force N of the plane on the block, and (iii) the static frictional force fs opposing the impending motion. In equilibrium, the resultant of these forces must be zero. Resolving the weight mg along the two directions shown, we have
mgsinθ=fs,mgcosθ=N
As θ increases , the self - adjusting frictional force fs increases unit at θ=θmax,fs achieves its maximum value (fs)max=μsN .
Therefore , tanθmax=μs or θmax=tan−1μs
When θ becomes just a little more than θmax , there is a small net force on the block and it begins to slide. Note that θmax depends only on µs and is independent of the mass of the block.
for θmax=15∘
μs=tan15∘
= 0.27
Topper's Solved these Questions
- LAW OF MOTIONBOOK - NCERT GUJARATICHAPTER - LAW OF MOTIONEXERCISE - EXERCISE
23 Videos
- LAW OF MOTIONBOOK - NCERT GUJARATICHAPTER - LAW OF MOTIONEXERCISE - EXERCISE (ADDITIONAL EXERCISE)
17 Videos
- KINETIC THEORYBOOK - NCERT GUJARATICHAPTER - KINETIC THEORYEXERCISE - ADDITIONAL EXERCISE
4 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - NCERT GUJARATICHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE
31 Videos
Similar Questions
A mass of 2kg rests on a horizontal plane. The plane is gradually inclined until at an angle θ=20∘ with the horizontal, the mass just begins to slides. What is the coefficient of static friction between the block and the surface ?
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
View Solution
Knowledge Check
A block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
A√3B12C1√2D1√3
A mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?

View SolutionA block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
View SolutionA mass of 4 kg rests on a horizontal plane. When the plane is gradually inclined to an angle 0 -15° with the horizontal, the mass just begins to slide. What is the coefficient of static friction between the block and the surface? [Given, tan 15° = 0.2679)
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View Solution
