Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).Solution in Gujrati
x=−2sin(3t+π/3)
x=cos(π/6−t)
x=3sin(2πt+π/4)
x=2cosπt
Step by step video & image solution for Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBOOK - NCERT GUJARATICHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- OSCILLATIONSBOOK - NCERT GUJARATICHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT GUJARATICHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- PHYSICAL WORLD BOOK - NCERT GUJARATICHAPTER - PHYSICAL WORLD EXERCISE - EXERCISES
8 Videos
Similar Questions
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
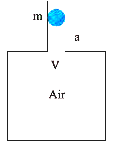
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].

View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can equal to 49 ms-1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5 ms−1 and the boy again throws the ball up with the maximum speed he can, how long goes the ball take to return to his hands ?
View SolutionSome of the most profound statements on the nature of science have come from Albert Einstein, one of the greatest scientists of all time. What do you think did Einstein mean when he said: "The most incomprehensible thing about the world is that it is comprehensible" ?
View SolutionPlot the corresponding reference circle for each of the following simple hoarmonic motions. Indicate the intial (t=0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case : (x is in cm and t is in s ). (a) x=-2 sin(3t+pi//3) (b) x=cos(pi//6-t) (c) x=3sin(2pit+pi//4) (d) x=2cospit
View SolutionPlot the corresponding SHM of particle. Indicate the intial (t=0) position of the particle, the radius of the circle and angular speed of the rotating particle. Consider sense of rotation to be anticlockwise and x in cm and t is in s. (a) =-2sin(3t(pi)/(3))
View SolutionPlot the corresponding SHM of particle. Indicate the intial (t=0) position of the particle, the radius of the circle and angular speed of the rotating particle. Consider sense of rotation to be anticlockwise and x in cm and t is in s. (b) x=cos((pi)/(6)-t)
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions, indicate the initial (t=0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anti clockwise in every case (x is cm and t is in s)
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions, indicate the initial (t=0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anti clockwise in every case (x is cm and t is in s)
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions, indicate the initial (t=0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anti clockwise in every case (x is cm and t is in s)
View SolutionPlot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t = 0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case : (x is in cm and t is in s). a) x=-2 sin (3t + pi//3) b) x= cos (pi//6 -t) c) x=3 sin (2pi t+ pi//4) d) x=2 cos pit .
View Solution
