Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t=0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case : (x is in cm and t is in s).
a) x=−2sin(3t+π/3)
b) x=cos(π/6−t)
c) x=3sin(2πt+π/4)
d) x=2cosπt.
If we express each function of the form x=acos(ωt+ϕ) …(i)
Where ϕ is the initial phase i.e., ϕ represents the angle which the initial radius vector of the particle makes· with the +ve direction of x-axis.
a) x=−2sin(3t+π3)=2cos(π2+3t+π3)
or x=2cos.(3t+5π6)
x=2cos(3t+5π6)
Comparing it with equation (i), we note that a=2ω=3andϕ=5π6.
Hence, the reference circle will be shown in Fig. (a).
b) x=cos(π6−t)=cos(t−π6) (∵cos(−θ)=cosθ)
Comparing it with equation (i), we note that a=1,ωandϕ=−π6
The reference circle will be as shown in Fig. (b).
c) x=3sin(2πt+π4)
=3cos(2πt+3π2+π4)
Comparing it with equation (i), we note that a=3,ω=2πandϕ=3π2+π4=7π4
The reference circle will be as in Fig. (c).
d) x=2cosπt
Comparing it with equation (i), we note that a=2,=πandϕ=0.
The reference circle will be as show in Fig. (d)

Similar Questions
Plot the corresponding reference circle for each of the following simple hoarmonic motions. Indicate the intial(t=0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case :(x is in cm and t is in s ).
(a) x=−2sin(3t+π/3) (b)x=cos(π/6−t) (c) x=3sin(2πt+π/4) (d) x=2cosπt
View SolutionPlot the corresponding reference circle for given SHM, indicate the initial (t=0) position of the paritcle, the radius of the circle , and the angular speed of the rotating paritcle. Consider anticlockwise direction for rotation. x=−3sin(2t+π4) (Express in the form , x= Acos ( omega t + phi)).
View Solution
Knowledge Check
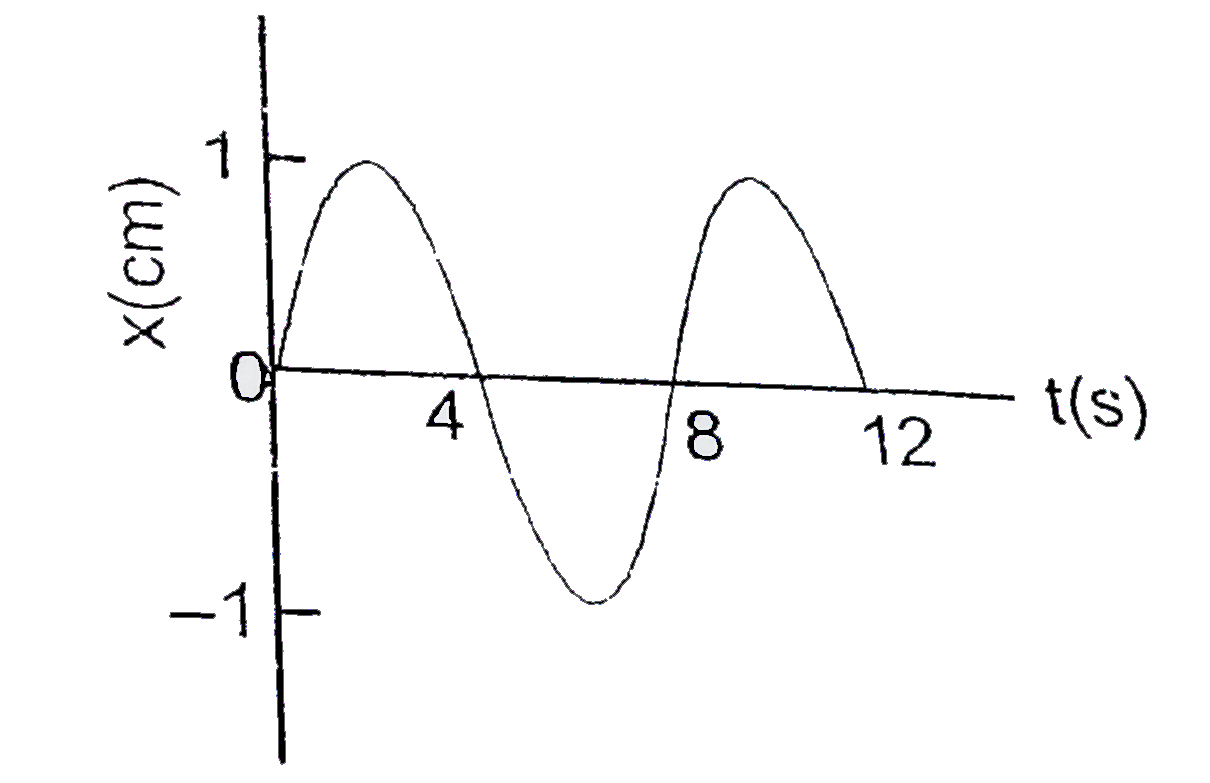
The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of t=4/3s is
 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2The x−t graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at t=4/3s is
 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
Plot the corresponding reference circle for given SHM, indicate the initial (t=0) position of the paritcle, the radius of the circle , and the angular speed of the rotating paritcle. Consider anticlockwise direction for rotation. x=−3sin(2t+π4) (Express in the form , x= Acos ( omega t + phi)).
View SolutionPlot the corresponding reference circle for given SHM x=2cos(π3−t) .Indicate the initial (t−0) position of the particle , the radius of the circle and the angular speed of the rotating particle . Consider anticlockwise direction for rotation.
Hint : x=2cos(π3−t)=2cos(t−π3) as cos(−θ)=cosθ . Compare with x=Acos(ωt+ϕ)
View SolutionPlot the corresponding reference circle for given SHM x=2cos(π3−t) .Indicate the initial (t−0) position of the particle , the radius of the circle and the angular speed of the rotating particle . Consider anticlockwise direction for rotation.
Hint : x=2cos(π3−t)=2cos(t−π3) as cos(−θ)=cosθ . Compare with x=Acos(ωt+ϕ)
View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=23s is

View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=23s is

View SolutionThe x−t graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at t=4/3s is

View Solution
