Figure 5.5 shows a small magnetised needle P placed at a point O. The arrow shows the direction of its magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.
(a) In which configuration the system is not in equilibrium?
(b) In which configuration is the system in (i) stable, and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown? 
Potential energy of the configuration arises due to the potential energy of one dipole (say, Q) in the magnetic field due to other (P). Use the result that the field due to P is given by the expression [Eqs. (5.7) and (5,8)]
BP=−μ0mp4πr3 (on the normal bisector)
Bp=μ024πmpr3 (on the axis)
where mp is the magnetic moment of the dipole P.
Equilibrium is stable when mQ is parallel to Bp and unstable when it is anti parallel to BP.
For instance for the configuration Q3, for which Q is along the perpendicular bisector of the dipole P, the magnetic moment of Q is parallel to the magnetic field at the position 3. Hence Q, is stable. Thus
(a) PQ1andPQ2
(b) (i) PQ3,PQ6(stable)(ii)PQ5,PQ4(unstable)
(c) PQ6
Topper's Solved these Questions
- MAGNETISM AND MATTERBook:NCERT GUJARATIChapter:MAGNETISM AND MATTERExercise:Exercises
Explore 25 Videos
- MAGNETISM AND MATTERBook:NCERT GUJARATIChapter:MAGNETISM AND MATTERExercise:Additional Exercises
Explore 19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT GUJARATIChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:EXERCISES
Explore 35 Videos
- MOVING CHARGES AND MAGNETISM Book:NCERT GUJARATIChapter:MOVING CHARGES AND MAGNETISM Exercise:ADDITIONAL EXERCISES
Explore 17 Videos
Similar Questions
Figure shows a small magnetised needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionFigure shows a small magnetized needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetized needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View Solution
Knowledge Check
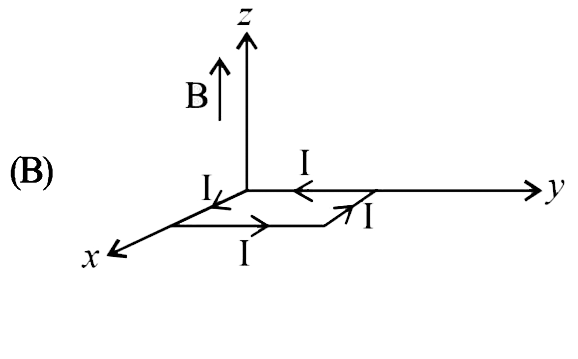
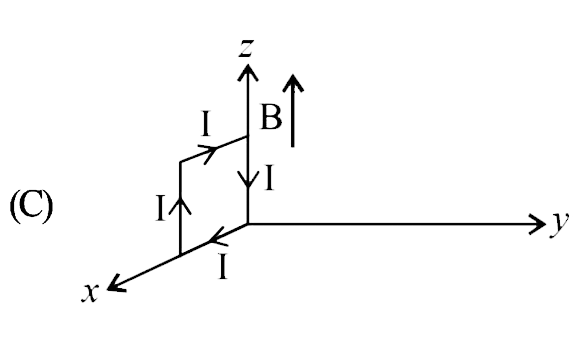
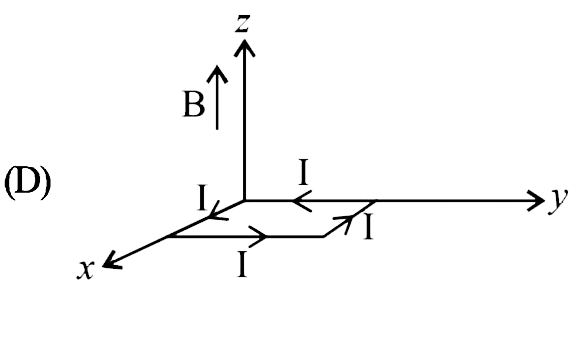
A rectangular loop of sides 10 cm and 5 cm carrying a current I of 12 A is placed in different orientations as shown in the figures below ,
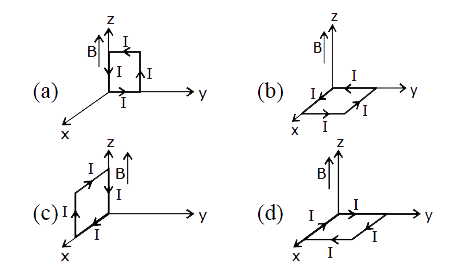
If there is a uniform magnetic field of 0.3 T in the positive z direction, in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?A(b) and (d), respectivelyB(b) and (c), respectivelyC(a) and (b), respectivelyD(a) and (c), respectively
Figure shows a small magnetised needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionConsider the situation shown in the diagram, where A small magnetised needle A is placed at a centre marked, as O. The direction of its mangetic moment I s indicated by arrow. The other arrow show different position (and orientations of the magnetic moment) of antoher identical magnetised eedle X.
In which configuration the system is not in equlibrium?
(ii) In which configuration is the system in (a) stable and (b) unsable equilibrium
(iii) Which configuration corresponds to the lowest potentials energy among all the configuration shown
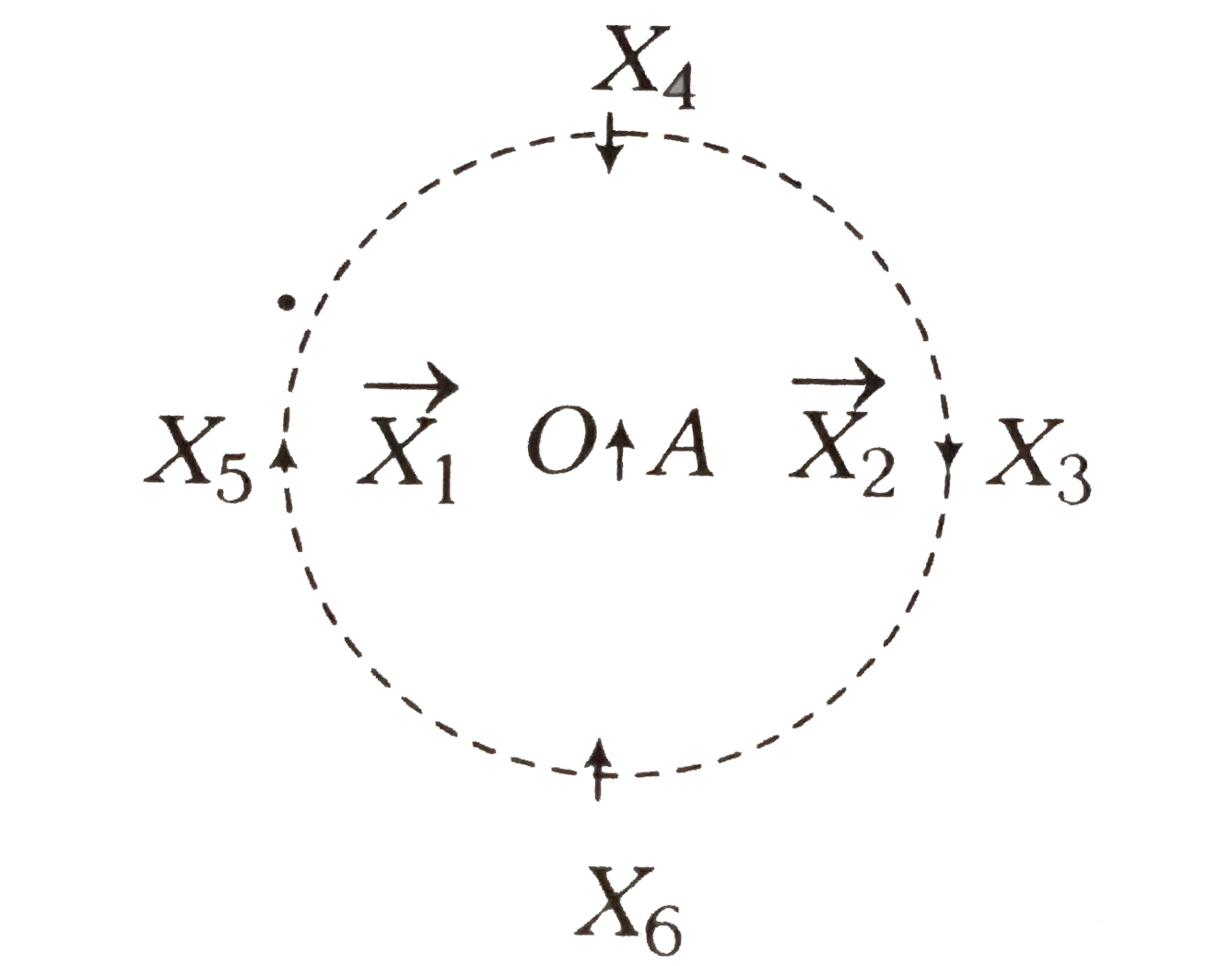
View SolutionConsider the situation shown in the diagram, where A small magnetised needle A is placed at a centre marked, as O. The direction of its mangetic moment I s indicated by arrow. The other arrow show different position (and orientations of the magnetic moment) of antoher identical magnetised eedle X.
In which configuration the system is not in equlibrium?
(ii) In which configuration is the system in (a) stable and (b) unsable equilibrium
(iii) Which configuration corresponds to the lowest potentials energy among all the configuration shown
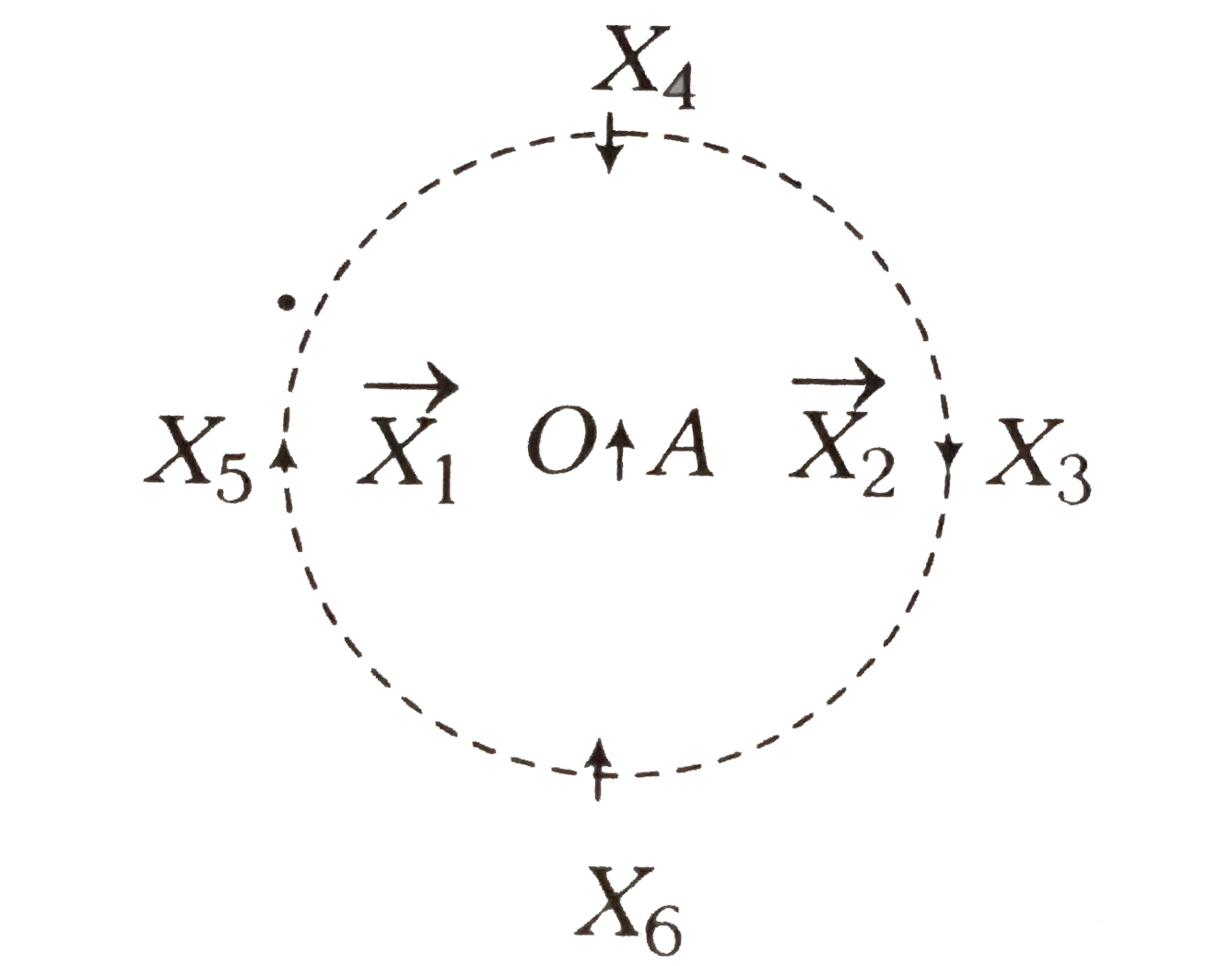
View SolutionFigure shows a small magnetised needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionFigure shows a small magnetised needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionIf there is uniform magnetic field of in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?
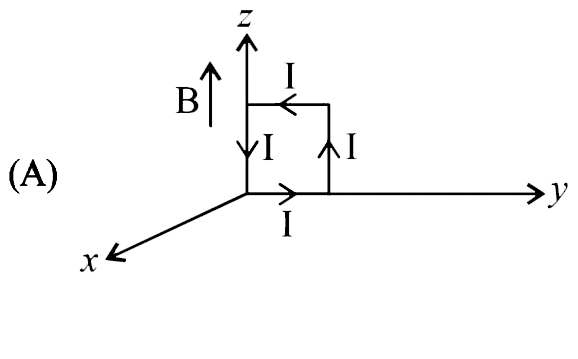
View SolutionA pivoted small magnetic needle of moment m is placed at a distance r along the axis of a short bar magnet of moment M. Find the force on the pivot of the needle.
View Solution
