A voltage V=V0sinωt is applied to a series LCR circuit. Derive the expression for the average power dissipated over a cycle.
Under what condition is (i) no power dissipated even though the current flows through the circuit, maximum power dissipated in the circuit ?
Applied voltage =V0sinωt
Current in the circuit =I0sin(ωt−ϕ)
where ϕ is the phase lag of the current with respect to the voltage applied,
Hence, instantaneous power dissipation
=V0sinωt×I0sin(ωt−ϕ)
=V0I02[2sinωt.sin(ωt−ϕ)]
=V0I02[cosϕ−cos(2ωt−ϕ)]
Therefore average power for one complete cycle = average of [V0I02{cosϕ−cos(2ω−ϕ)}]
The average of the second term over a complete cycle is zero.
Hence, average power dissipated over one complete
cycle =V0I02cosϕ
Conditions :
(i) No power is dissipated when R = 0 (or ϕ=90∘)
[NOte : We can also write, this condition cannot be satisfied LCR circuit..]
(ii) Maximum power is dissipated when XL=XC
or ωL=1ωC (or ϕ=0)
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - OSWAAL PUBLICATIONCHAPTER - ALTERNATING CURRENTEXERCISE - Topic - 2 (Long answer Type Questions)
4 Videos
- ALTERNATING CURRENTBOOK - OSWAAL PUBLICATIONCHAPTER - ALTERNATING CURRENTEXERCISE - Topic - 2 (Numerical Problem)
11 Videos
- ALTERNATING CURRENTBOOK - OSWAAL PUBLICATIONCHAPTER - ALTERNATING CURRENTEXERCISE - Topic - 2 (Short Answer Type Questions -I)
3 Videos
- 2020 Solved Paper I BOOK - OSWAAL PUBLICATIONCHAPTER - 2020 Solved Paper I EXERCISE - Exercise
41 Videos
- ATOMSBOOK - OSWAAL PUBLICATIONCHAPTER - ATOMSEXERCISE - NUMERICAL PROBLEMS
11 Videos
Similar Questions
A voltage V=Vmsinωt is applied to a series L-C-R circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit ?
View SolutionA voltage V=V0sinωt is applied to a series LCR circuit. Derive expression for the average power dissipated over a cycle.
Under What condition (i) no power is dissipated even though the current flows through the circuit?
(ii) Maximum power is dissipated in the circuit?
View Solution
Knowledge Check
If in the circuit, power dissipation is 150 W. then R is
 A2ΩB6ΩC5ΩD4Ω
A2ΩB6ΩC5ΩD4ΩIn the series LCR circuit, the power dissipation is through
ARBLCCDBoth L and C
A voltage V=V0sinωt is applied to a series LCR circuit. Derive expression for the average power dissipated over a cycle.
Under What condition (i) no power is dissipated even though the current flows through the circuit?
(ii) Maximum power is dissipated in the circuit?
View SolutionDerive the expression for the power dissipated by an ideal resistor in an AC circuit .
View SolutionIf in the circuit, power dissipation is 150 W, then R is :
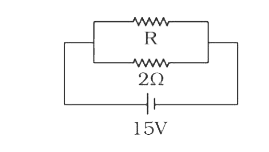
View SolutionIf in the circuit, power dissipation is 150 W, then R is :

View SolutionIf in the circuit , power dissipation is 150 W, then R is
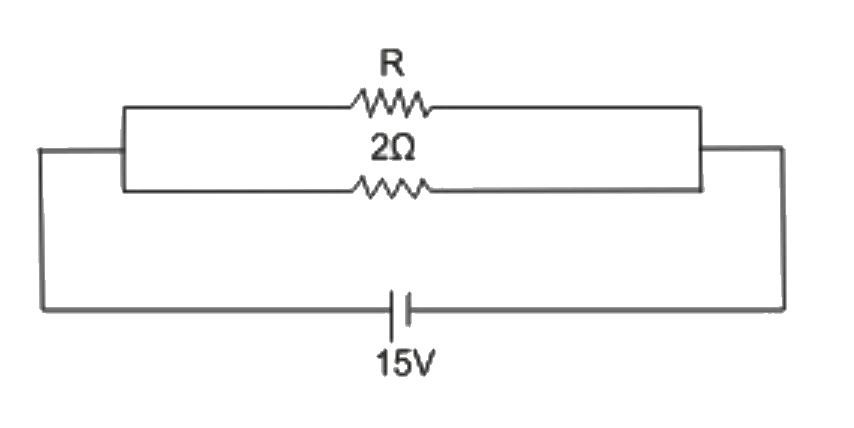
View SolutionThe average power in LCR series circuit is
View Solution
