A series LCR circuit is connected to an a.c. source having voltage V=Vmsinωt. Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
Obtain the condition for resonance to occur. Define 'power factor'. State the conditions under which it is (i) maximum and (ii) minimum.
From the phasor diagram we have
V2m=V2Rm+(VCm−VLm)2
=i2m[R2+(XC−XL)2]
im=Vm√R2+(XC−XL)2

The current is seen to lead the voltage by an angle ϕ where
tanϕ=XC−XLR
Hence i=imsin(ωt+ϕ)
Where
im=Vm√R2+(XC−XL)2
and ϕ=tan−⎡⎢
⎢⎣(ωL−1ωC)R⎤⎥
⎥⎦
Condition of resonance : ωL−1ωC=0
or ωL=1ωC or ω=1√LC
Power factor equals the cosine of the phase angle power factor i.e., power factor,
cosϕ=RZ
Power factor is maximum when cosϕ=1 i.e., when R = Z or XL=XC.
Power factor is minimum when cosϕ=0 i.e., when R=0.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - OSWAAL PUBLICATIONCHAPTER - ALTERNATING CURRENTEXERCISE - Topic - 2 (Numerical Problem)
11 Videos
- ALTERNATING CURRENTBOOK - OSWAAL PUBLICATIONCHAPTER - ALTERNATING CURRENTEXERCISE - Topic - 3 (Very Short Answer Type Questions)
3 Videos
- ALTERNATING CURRENTBOOK - OSWAAL PUBLICATIONCHAPTER - ALTERNATING CURRENTEXERCISE - Topic - 2 (Short Answer Type Questions -II)
7 Videos
- 2020 Solved Paper I BOOK - OSWAAL PUBLICATIONCHAPTER - 2020 Solved Paper I EXERCISE - Exercise
41 Videos
- ATOMSBOOK - OSWAAL PUBLICATIONCHAPTER - ATOMSEXERCISE - NUMERICAL PROBLEMS
11 Videos
Similar Questions
A series LCR circuit is connected to an a.c. source having voltage V=Vmsinωt
Derive the expression for the instantaneous current I and its phase relationship to the applied voltage. Obtain the condition for resonance to occur. Define 'power factor'. State the conditions under which it is (i) maximum, (ii) minimum.
View SolutionA series LCR circuit is connected to a source having voltage v=vmsinωt.Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
Obtain the condition for resonance to occur.Define 'power factor'.State the conditions under which it is (i)maximum and (ii)minimum.
View Solution
Knowledge Check
A series LR circuit is connected to a voltage source with V(t) = V0 sin ω t. after very large time, current I(t) behaves as (t0>>LR)
A B
B C
C D
D
An ac source of voltage V=Vmsinωt is connected across the resistance R as shown in figure. The phase relation between current and voltage for this circuit is
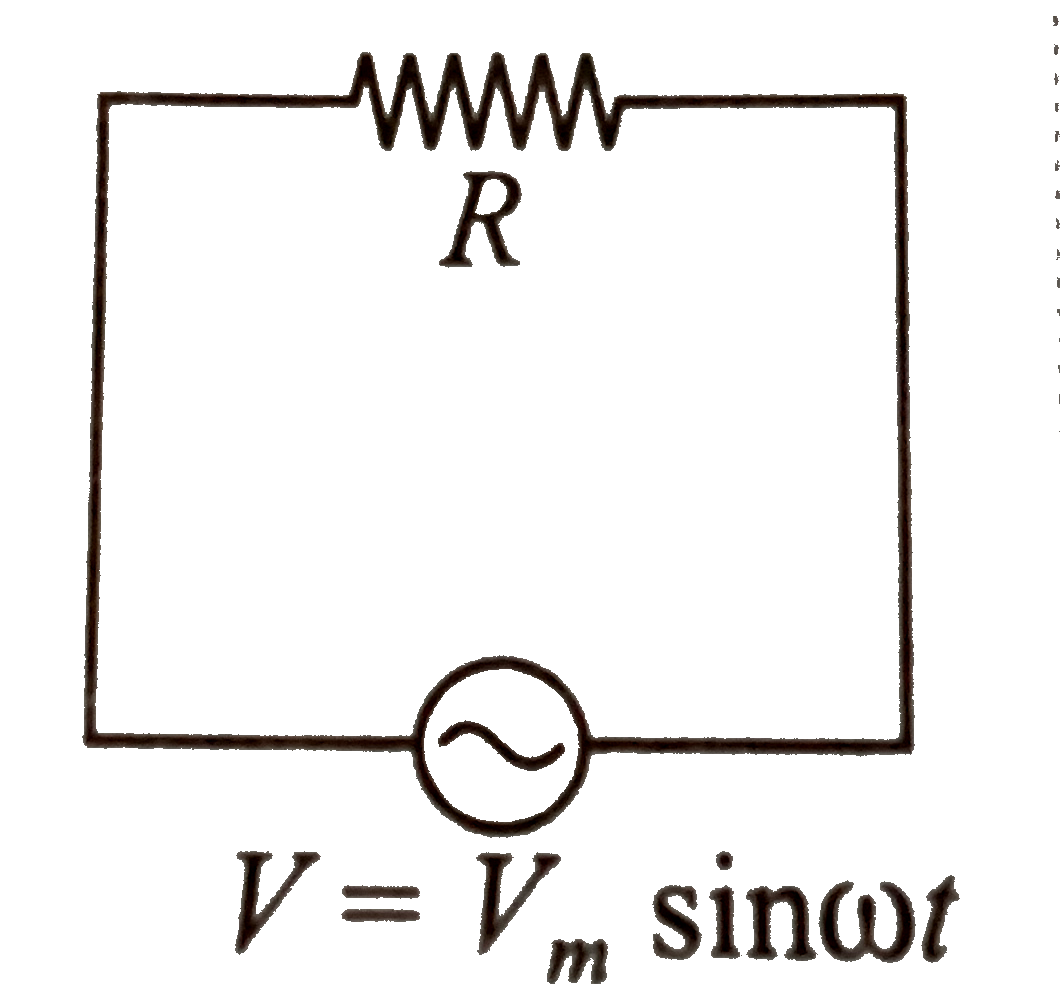 Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘An ac source of voltage V=Vmsinωt is connected across the resistance R as shown in figure. The phase relation between current and voltage for this circuit is
 Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
State the conditions under which power factor is (i) maximum, and (ii) minimum.
View SolutionDraw the phasor diagram of a series LCR connected across an ac source V=V0sinωt. Hence derive the expression for the impedance of the circuit . Obtain the conditions for the phase angle under which the current is (i) maximum and (ii) minimum.
View SolutionIn a series LCR circuit connected to an a.c. source of variable frequency and voltage V=Vmsinωt draw a plot showing the variation of current (I) with angular frequency (w) for two different values of resistance R1 and R2(R1>R2). Write the condition under which the phenomenon of resonance occurs. For which value of the resistance out of the two curves, a sharper resonance is produced ? Define Q-factor of the circuit and give its significance.
View SolutionAn a.c. voltage V=Vm sin ot is applied across an inductor L. Obtain an expression for current I.
View SolutionAn L.C, R series circuit is connected to ac, source. At resonance, the applied voltage and the current flowing through the circuit will have a phase difference of
View Solution
