Trace the ays of light showing the formation of an image due to a point object placed on the axis of a spherical surface separating the two media of refractive indices n1andn2. Establish the relation between the distance of the object, the image and the radius of curvature from the central point of the spherical surface.
Hence derive the expression of the lends maker's formula
Refraction of shperical surface: (a) Sign conventions :
(i) All distances are measured from the pole of the spherical surface.
(ii) Distance measured in the direction of incident light are taken positive.
(iii) Distances measured in the opposite direction of incident light are negative.
Assumptions :
(i) The object is a point object placed on the principal axis.
(ii) APerture of the refracing surface is small.
(iii) Angle of incidence and angle of refraction are small.
I is the real image of a point O placed on the principal axis of spherical surface with centre of curvature C, the radius of curvature R. The rays are incident from a medium of refractive index n1 to refractive index n2.
For samll aperture, NM will be taken to the length of the perpendicular from N to principal axis.
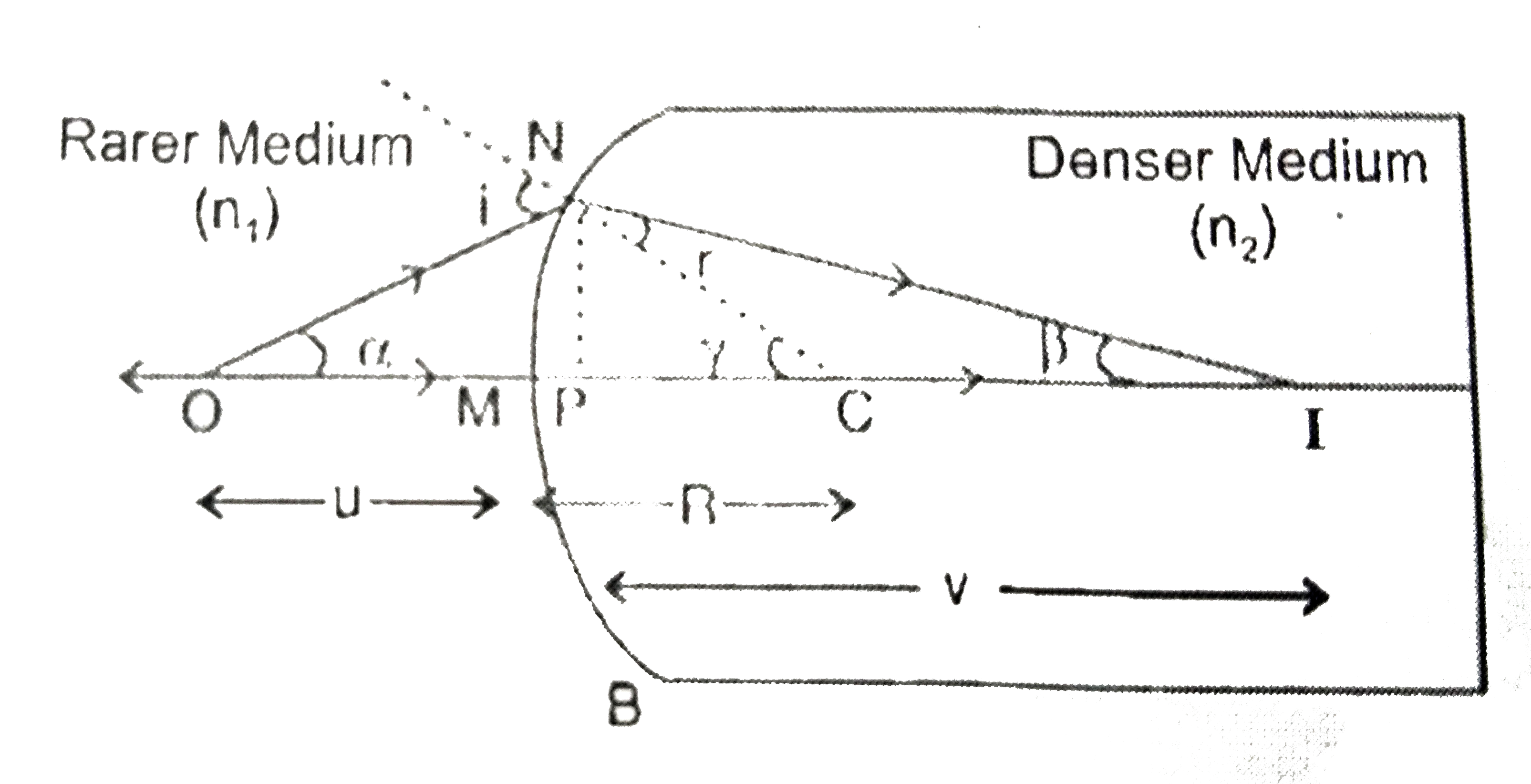
We have, For small angles
tan∠NOM=∠NOM=MNOM
tan∠NCM=∠NCM=MNMC
tan∠NIM=∠NIM=MNMI
Exterior angle i=∠NOM+∠NCM
i=MNOM+(MN))MC..(i)
and r=∠NCM−∠NIM
r=MNMC−MNMI...(ii)
By Snell's law sinisinr=n2n1
For small angles, ir=n2n1
∴n1i=n2r ...(iii)
Putting the values of i and r in eq. (iii)
n1(MNOM+MNMC)=n2(MNMC−MNMI)
Dividing by MN
n1OM+n1MC=n2MC−n2MI⇒n1OM+n2MI=n2MC−n1MC⇒n1OM+n2MI=n2−n1MC
Using Cartesian sign convention,
OM=−u,MI=+v,MC=+R ∴n1−u+n2v=n2−n1R
or n2v−n1u=n2−n1R
(b) Lens Maker's Formula : The image of point object O is formed in two steps. The first reflecting surface forms the image I, of the object O. The image I1 acts as a virtual object for formation of image I by the second surface.
For the first surface ABC
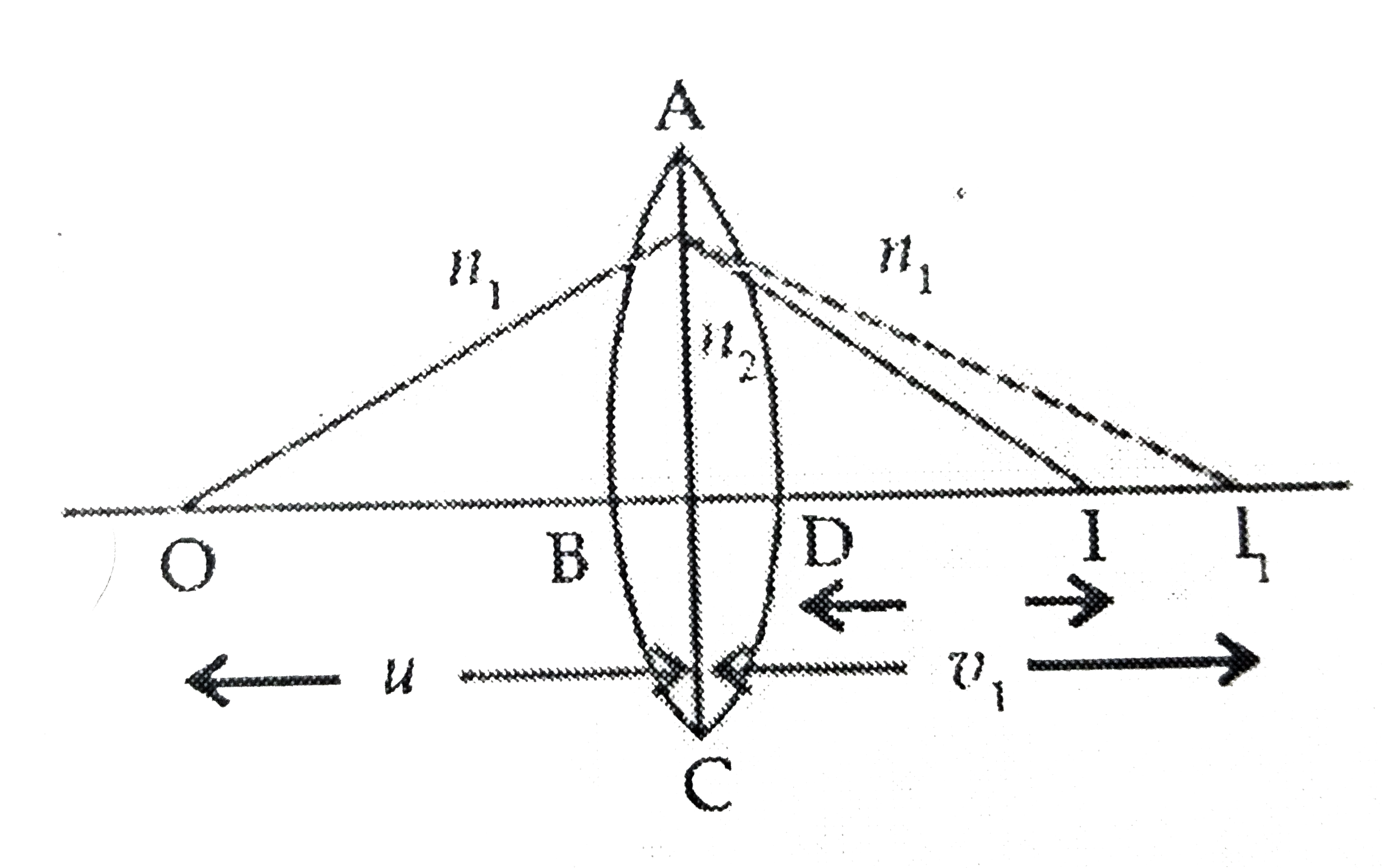
[∵−n1U+n2V=n2−n1R]
−n1OB+n2BI1=n2−n1BC1..(i)
For the second surface ADC
−n1DI1+n2DI=n2−n1DC2
For a thin lens, BI1=DI1
∴−n2BI1+n1DI=n2−n1DC2..(ii)
On adding eq. (i) and (ii), we get, −n1OB+n1DI=(n2−n1)[1BC1+1DC2]
If the object is at infinity ∴OB=∞ and I is at the focus of the lens ∴DI=f (focal length of convex lens]
−n1∞+n1f=(n2−n1)[1BC1+1DC2]
By the sign convention, BC1=+R1andDC2=−R2
∴n1f=(n2−n1)(1R1−1R2)⇒1f=(n2n1−n1R2)(1R1−1R2)⇒1f=(n21−1)(1R1−1R2)
1f=(n−1)(1R1−1R2)
where n21=n, is the refractive index of material of the lens w.r.t. air
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET II
9 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET III
9 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION - B
9 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface.
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
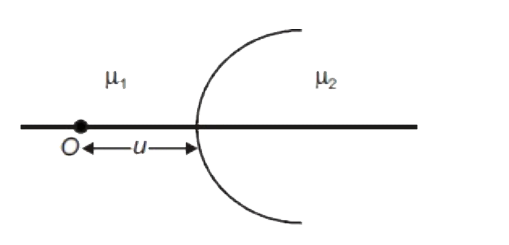
View Solution
Knowledge Check
The diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
 AReal image will form if μ1>μ2 and for all values of uBReal image for some values of u if μ1>μ2CVirtual image will form if μ1>μ2DVirtual image will form if μ1<μ2
AReal image will form if μ1>μ2 and for all values of uBReal image for some values of u if μ1>μ2CVirtual image will form if μ1>μ2DVirtual image will form if μ1<μ2A convex spherical refracting surfaces separates two media glass and air (μg=1.5). If the image is to be real, at what minimum distance u should the object be placed in air if R is the radius of curvature
Au>3RBu>2RCt–4RDt–RIn the figure, a point object O is placed in air. A spherical boundry separates two media of radius of curvature 1.0m. AB is principal axis. The separation between the images formed due to refraction at spherical surface is
 A12mB20mC14mD10m
A12mB20mC14mD10m
A convex spherical refracting surfaces separates two media glass and air (μg=1.5). If the image is to be real, at what minimum distance u should the object be placed in air if R is the radius of curvature
View SolutionIn the figure, a point object O is placed in air. A spherical boundry separates two media of radius of curvature 1.0m. AB is principal axis. The separation between the images formed due to refraction at spherical surface is

View SolutionA concave spherical surface of radius of curvature 100 cm separates two media of refractive indices 1.50 and 43. An object is kept in the first medium at a distance of 30 cm from the surface. Calculate the position of the image.
View SolutionA concave spherical surface of radius of curvature 100 cm separates two media of refractive indices 1.50 and 43. An object is kept in the first medium at a distance of 30 cm from the surface. Calculate the position of the image.
View Solution(a) A point object is placed on the principal axis of a convex spherical surface of radius of curvature R, which separates the two media of refractive indices nx and n2(n2>n1)
Draw the ray diagram and deduce the relation between the object distance (w), image distance (v) and the radius of curvature (R) for refraction to take place at the convex spherical surface from rarer to denser medium.
(b) A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1.6. If it is immersed in a liquid of refractive index 1.3, find its new focal length.
View Solution
