A series LCR circuit is connected to an ac source having voltage $v = v_{m} sin ω t$ . Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
(i) Maximum and (ii) minimum.

Text Solution

Verified by Experts

(a) (1) Equivalent impendance (Z) is LCR circuit: The effective resistance offered by a series LCR-circuit is called its impedance. It is denoted by Z.
Suppose an inductance L, capacitance C and resistance R are connected in series to a source of alternating emf, $V = V_{0}$ sin wt.
Let, I be the instantaneous value of current in the series circuit.
Then voltages across the three components are
(i) $V_{L} = X_{L} I$ It is ahead of current I in phase by $90^{\circ}$ .
(ii) $V_{C} = V_{C} I$ . it lags behind the current I in phase by $90^{\circ}$ .
(iii) $V_{R} = R I$ . It is in phase with current I.

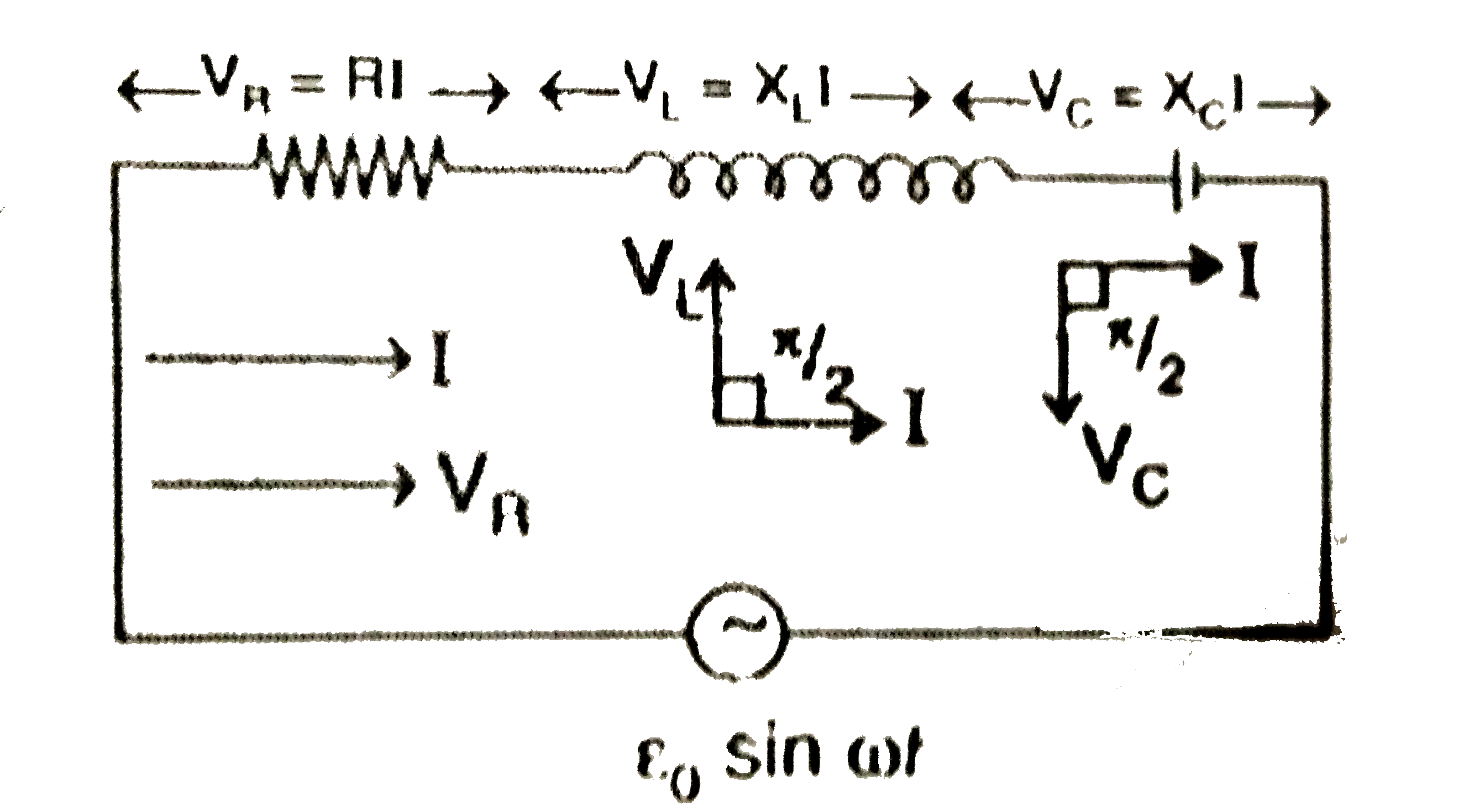
These voltages are shown in the phasor diagram given below :

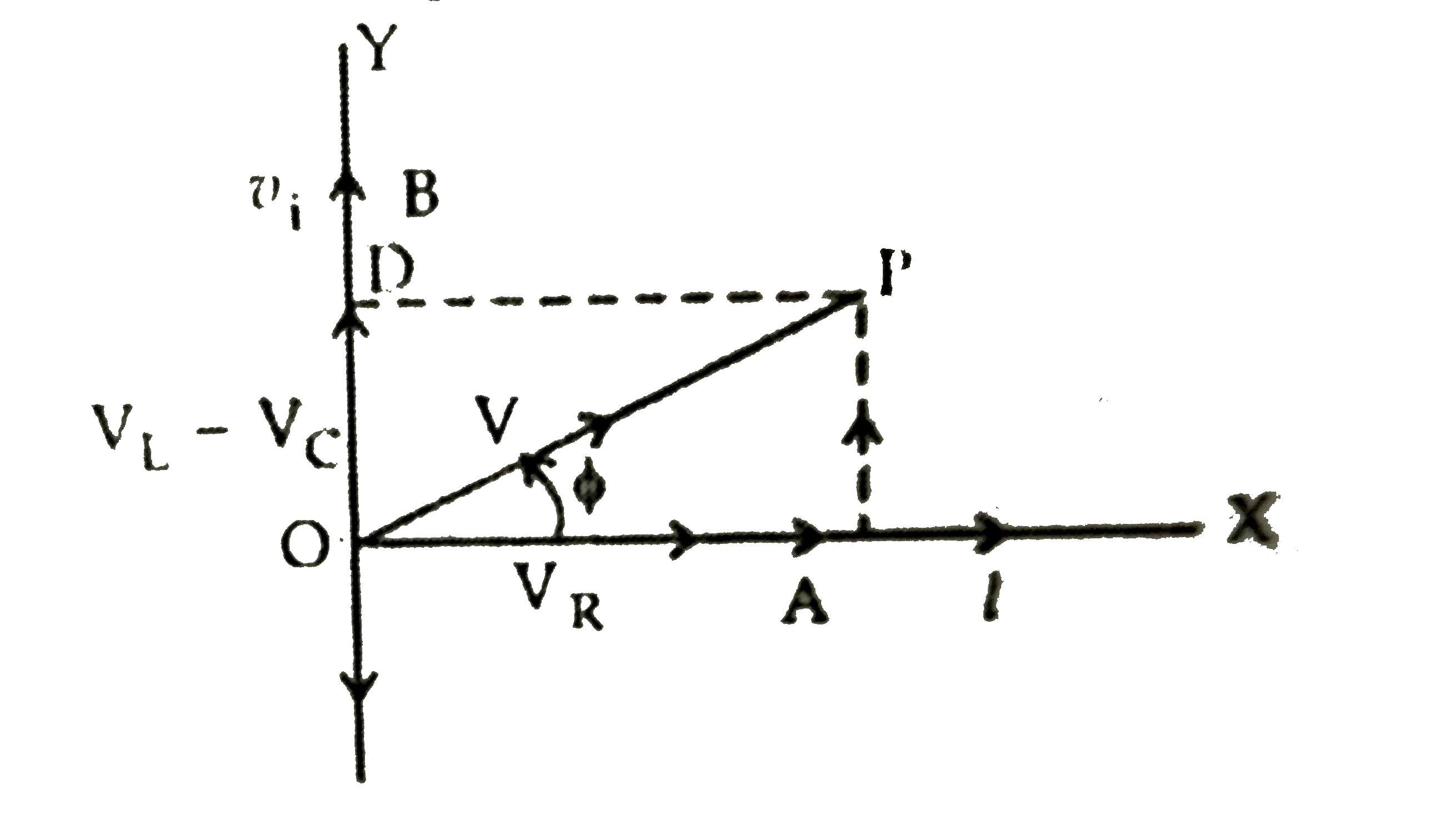
As $V_{L} and L_{C}$ are in opposite directions, their resultant is $O D = V_{L} - V_{C}$ , in the positive y-direction By paralllelogram law, the resultant voltage is $V = O P$
$= \sqrt{O A^{2} + O D^{2}} = \sqrt{V_{R}^{2} + {(V_{L} - V_{C})}_{L}^{2}}$
$= \sqrt{R^{2} I^{2} + {(X_{L} I - X_{C} I)}_{L}^{2}} = I \sqrt{R^{2} + {(X_{L} - X_{C})}_{L}^{2}}$
$∴ \frac{V}{I} = \sqrt{R^{2} + {(X_{L} - X_{C})}_{L}^{2}}$ .
Clear, $V / I$ is the effective resistance of the series LCR circuit and is called its impedance (Z).
$∴ Z = \sqrt{R^{2} + {(X_{L} - X_{C})}_{L}^{2}} = \sqrt{R^{2} + {(Ω L - \frac{1}{Ω C})}^{2}} [\begin{matrix} ∵ X_{L} = Ω L X_{C} = 1 / Ω C \end{matrix}]$
(2) When Z=R, then $X_{1} = X_{C}$
$∴ Ω L = \frac{1}{Ω C} \Rightarrow Ω^{2} L C = 1 \Rightarrow Ω = \frac{1}{\sqrt{L C}}$
(3) , From phasor diagram, it follows that in LCR series circuit, V leads I $(X_{L} > L_{C})$ by phase angle $ϕ$ then
$tan ϕ = \frac{A P}{O A} = \frac{V_{L} - V_{C}}{V_{R}}$
$tan ϕ = \frac{I X_{L} - I X_{C}}{I R} \Rightarrow tan ϕ = \frac{X_{L} - X_{C}}{R}$
$tan ϕ = \frac{Reactive Impedance}{Resistance}$
$∴ ϕ = {tan}^{- 1} [\frac{Reactive Impedance}{Resistance}]$
$∵ Impedance Z = \sqrt{R^{2} + {(X_{L} - X_{C})}_{L}^{2}}$
For resonance, $X_{L} = X_{C} ∴ Z = \sqrt{R^{2}} \Rightarrow Z = R$
Hence, for the condition of resonance, impedance is equal to resistance.
Power factor : Power factor is defined as the ratio of true power to apparent power. it is denoted by $cos ϕ$ .
$∴ Power factor cos ϕ = \frac{R}{\sqrt{R^{2} + {(X_{L} - X_{C})}_{L}^{2}}}$
(i) Power factor is maximum when the circuit contains only R.
(ii) Power factor is minimum for purely inductive or capacitive circuit.

Updated on:21/07/2023

A series LR circuit is connected to a voltage source with V(t) = $V_{0}$ sin $ω$ t. after very large time, current I(t) behaves as $(t_{0} > > \frac{L}{R})$
A
B
C
D
An ac source of voltage $V = V_{m} sin ω t$ is connected across the resistance R as shown in figure. The phase relation between current and voltage for this circuit is

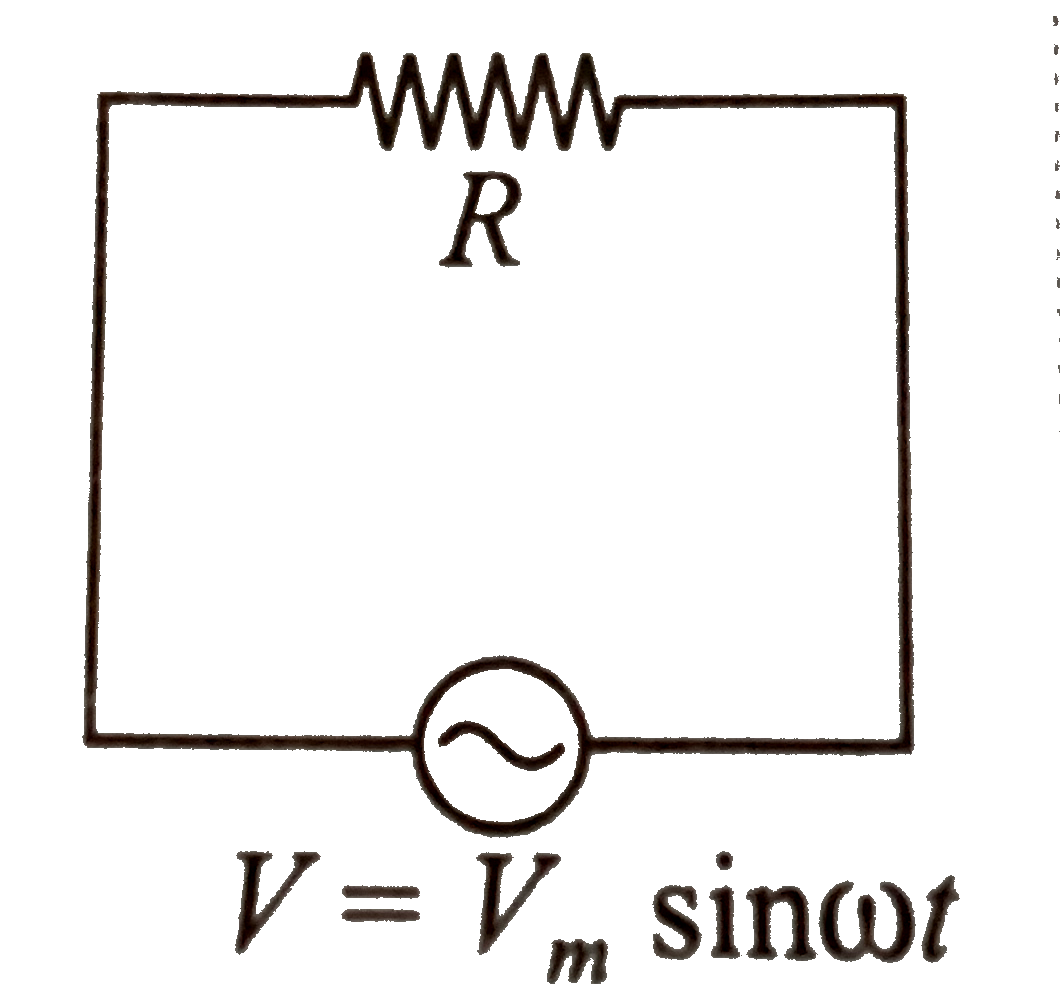Aboth are in phase
Bboth are out of phase by $90^{\circ}$
Cboth are out of phase by $120^{\circ}$
Dboth are out of phase by $180^{\circ}$
An ac source of voltage $V = V_{m} sin ω t$ is connected across the resistance R as shown in figure. The phase relation between current and voltage for this circuit is

Aboth are in phase
Bboth are out of phase by $90^{\circ}$
Cboth are out of phase by $120^{\circ}$
Dboth are out of phase by $180^{\circ}$